

umwelt-online: TRB 610 - Druckbehälter Aufstellung von Druckbehältern zum Lagern von Gasen
 |
zurück |  |
| Geometrische Darstellungen der explosionsgefährdeten Bereiche nach Abschnitt 4.2.1.1.2; | Anlage 4 zu TRB 610 |
Bild 1 Aufstellung im Freien, Gas leichter als Luft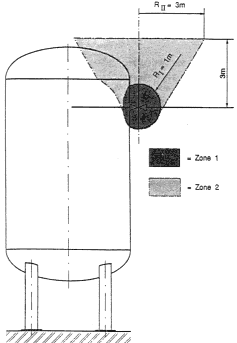 |
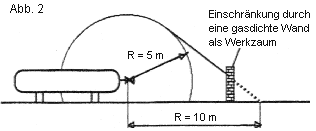
Bild 2 Aufstellung im Freien, Gas schwerer als Luft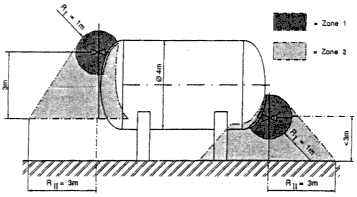 |
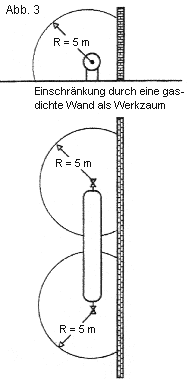
Bild 3 Aufstellung im Freien, Gas gleich schwer wie Luft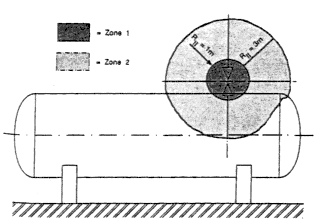 |
Bild 4 Erdgedeckte Aufstellung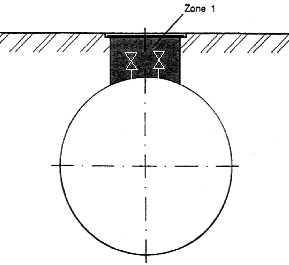 |
| Festlegung der Schutzabstände nach Abschnitt 3.2.3.3.1 für Lagerbehälter bei vorhandenen Brandlasten 00a | Anlage 5 zu TRB 610 |
Der Schutzabstand zwischen Brandlast und Lagerbehälter ergibt sich aus dem Diagramm zu Anlage 5 in Abhängigkeit von der zulässigen Werkstofftemperatur.
Als zulässige Werkstofftemperatur wird die Temperatur eingesetzt, bei der die Sicherheit gegen die Streckgrenze gleich 1 wird. Man erhält sie, indem man die Streckgrenze bei der zulässigen Betriebstemperatur durch den Sicherheitsbeiwert (im allgemeinen 1,5) dividiert und mit diesem Streckgrenzenwert aus den Werkstofftabellen die zugehörige Temperatur bestimmt.
Beispielhaft sind in der folgenden Tabelle für 8 Werkstoffe die entsprechenden Werte aufgeführt.
| Stahlsorte | Streckgrenze bei Raumtemp. K [N/mm2] |
K/S mit S = 1,5 [N/mm2] |
zul. Werkstoff- temperatur [°C] |
|
| Kurzname | Werkstoff-Nr. | |||
| C 22.3 | 1.0427 | 220 | 147 | 258 |
| C 22.8 | 1.0460 | 240 | 160 | 262 |
| St 35.8 | 10305 | 235 | 157 | 266 |
| RSt 37.2 | 1.0038 | 205 | 137 | 267 |
| HI | 1.0345 | 235 | 157 | 266 |
| HII | 1.0425 | 265 | 177 | 264 |
| WStE 355 | 1.0565 | 355 | 237 | 245 |
| 15Mo3 | 1.5415 | 285 | 190 | 325 |
Diagramm Schutzabstand als Funktion der zulässigen Werkstofftemperatur
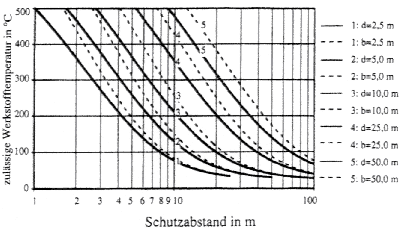
| Randbedingungen: | Flammenintensität 10 W/cm2 (z.B. Dieselkraftstoff); Brandfläche π · (d/2)2 oder b · b im m2 |
Das Diagramm "Schutzabstand als Funktion der zulässigen Werkstofftemperatur" wurde für das Brandmedium Dieselkraftstoff in Abhängigkeit von Brandlastdurchmesser d (runde Brandlasten) bzw. Brandlastbreite b (eckige Brandlasten) berechnet. Da nur wenige Stoffe, z.B. Pentan, eine größere Flammenintensität (emittierte Wärmestrahlung > 10 W/cm2) als Dieselkraftstoff haben, sind Brände von z.B. Kunststoff, Holz, Stroh aufgrund ihrer geringeren Flammenintensität bzw. der kurzen Branddauer bei der Abstandsbemessung durch das Diagramm abgedeckt. Weiterhin würden bei der Berechnung des Diagramms die Flammenlänge (Wirksame Flammenhöhe) sowie die Brandlasttiefe integriert und können bei der praktischen Anwendung unberücksichtigt bleiben.
Ist Flammenberührung vermieden, kann der Einfluß des Windes auf die Flammengeometrie vernachlässigt werden, da mit den Bemessungen für das Diagramm die maximale Einstrahlung berücksichtigt ist.
Brandlasten oberhalb der Scheitelhöhe des Behälters, z.B. Dachstuhlbrand, sind durch die vorliegenden Werte abgedeckt, da die Einstrahlwerte in diesen Fällen geringer sind.
Bei der Ermittlung des erforderlichen Schutzabstandes ist die Größe des Lagerbehälters und die Stellung/Aufstellung des Behälters vernachlässigbar. Entscheidend ist der Punkt des Behälters, der der Brandlast am nächsten liegt, da die Strahlungsintensität auf den Behälter mit dem Quadrat der Entfernung abnimmt. Aus diesem Grunde sind die erforderlichen Schutzabstände zu runden Brandlasten generell geringer als zu eckigen Brandlasten - siehe Bild 1 zu Anlage 5.
Bild 1 zu Anlage 5
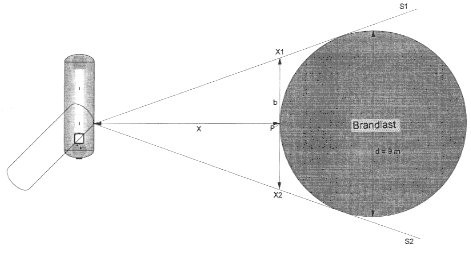
Bei außermittiger Anordnung der Lagerbehälter zu eckigen Brandlasten - siehe Bild 2 zu Anlage 5, Fall 2 und 3 - sind die erforderlichen Schutzabstände aus dem Diagramm über die Hilfsbreiten b1 zu bestimmen.
Bild 2 zu Anlage 5
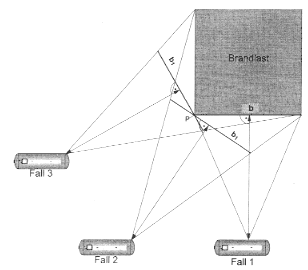
Hat die Brandlast eine größere Flammenintensität als Dieselkraftstoff oder sollen die Abstände zur Brandlast genau berechnet werden, so kann dies nach dem erstellten Rechnungsprogramm [2] erfolgen.
Die Bemessung des Sicherheitsventils muß für den Wärmeeintrag bei der ermittelten zul. Werkstofftemperatur so erfolgen, daß ein Druckanstieg über den Auslegungsdruck des Lagerbehälters hinaus nicht möglich ist - siehe Anlage 6.
Basis für die genannten Bemessungen sind Brandlastversuche an Flüssiggaslagerbehältern, die in [1] zusammengefaßt und in [2] und [3] ausgewertet sind.
| Beispiel: |
| Werkstoff Lagerbehälter: H II |
| zulässige Werkstoffternperatur: 264°C |
| Brandlast: Kunststoff |
| Brandlastbreite b = 5 m |
| Schutzabstand =6,1 m |
Literatur*):
[1] Gas-Wärme-Institut, Bericht Nr. 8112 vom 09.04.1990, "Brandlast/Strahlungsversuche zur Ermittlung von Mindestabständen von Druckbehältern für Flüssiggas nach DIN 51622 zu möglichen Brandherden".
[2] Technische Überwachung, BD 32 (1991), Nr. 4, S. 142 ff., "Lagerung brennbarer Stoffe - Berechnung von erforderlichen Abständen zu möglichen Brandlasten".
[3] "Flüssiggas" Heft 5/91, Strobel-Verlag Arnsberg
| Bemessung der Abblaseleistung von Sicherheitsventilen bei Wärmeeintrag in einen Lagerbehälter infolge Wärmestrahlung | Anlage 6 zu TRB 610 |
Wird bei Lagerbehältern die zul. Betriebstemperatur - höchstmögliche Temperatur des Beschickungsgutes (siehe TRB 801, Nr. 27 Absch. 3.5) z.B. durch Wärmestrahlung bei einem Brand, überschritten, so wird auf Grund des Anstieges des Dampfdruckes des Gases der Ansprechdruck des Sicherheitsventiles überschritten. Die höchsten Temperaturen stellen sich - abhängig vom Wärmeeintrag - an der nicht mit verflüssigtem Gas gekühlten Behälteroberfläche ein, da an diesen Stellen eine Wärmeabfuhr nur durch die Gasphase erfolgt. An diesem Teil der Behälterwandung darf höchstens die zulässig Werkstofftemperatur erreicht werden. Diese Temperatur ergibt sich aus der Berechnung mit dem Sicherheitsbeiwert S = 1 gegen die Streckgrenze (s. Anlage 5). Abgeleitet aus den geometrischen Verhältnissen bei der Bestrahlung eines Behälters mit einer Wärmequelle und der konservativen Annahme, daß
erhält man aus der Wärmebilanz den entsprechenden verdampfenden Massestrom des verflüssigten Gases. Diesen Massestrom muß das Sicherheitsventil in der Lage sein abzuführen. Mit weiteren Annahmen zur sicheren Seite hin erhält man folgende Gleichung:
| m' = 1,063 ⋅ t1,64 ⋅ A/r l0-3 | |
| mit | m' = abzuführender Massestrom [kg/sec] |
| t = zulässige Werkstofftemperatur [°C] | |
| a = bestrahlte Behälterfläche = d ⋅ l | |
| d = Durchmesser des Behälters [m] | |
| I = Lange des Behälters [m] | |
| r = Verdampfungswärme des Gases [kJ/kg] |
Stellt man die Gleichung um zu
(m' ⋅ r) / a = 1,063 . t1,64 l0-3
erhält man das nachfolgende Diagramm.
Diagramm zu Anlage 6: Mengenbemessungen für Abblaseleistungen von Sicherheitsventilen bei durch Wärmebelastung beaufschlagten Behältern

Oberflächentemperatur des bestrahlten Behälters
(zulässige Werkstofftemperatur in °C)
Ergeben sich danach zu große Sicherheitsventile, so ist eine genauere Berechnung mit den entsprechenden Randbedingungen erforderlich (s. Literatur Anlage 5).
Beispiele:
Erforderliche Abblaseleisoung eines Sicherheitsventiles an einem
1. Lagerbehälter für Propan
Die hypothetische Brandlast soll zu der zulässigen Werkstofftemperatur (Oberflächentemperatur im Bereich der Gasphase) von 250 °C am Lagerbehälter führen, was bei
eine Temperatur von 42 °C in der Flüssigphase des Gases ergibt (s. GWI-Bericht; die Kühlung durch Verdampfung des Gases hält die Flüssigphase auf der Temperatur von 42 °C; bei einer Bemessung des Sicherheitsventiles mit den oben zugrunde gelegten Vorgaben ist immer eine dem Abblasedruck des Gases - d.h. dem Einstelldruck des Sicherheitsventiles - entsprechende Temperatur gegeben.).
| Einstelldruck des Sicherheitsventiles: | p = 15,6 bar |
| Verdampfungsenthalpie von Propan bei 42 °C: | r = 309 kJ/kg |
| Länge des Behälters: | 1 = 4,8 m |
| Durchmesser des Behälters: | d = 1,25 m |
| Aus der Gleichung bzw. dem Diagramm ergibt sich bei 250 °C | |
(m' ⋅ r) / a = 9,1,
daraus folgt die über das Sicherheitsventil abzuführende Menge mit
| m' | = 9,l ⋅ A/r = 9,l ⋅ 6/309 |
| = 0,177 kg/sec | |
| = 636 kg/h |
2. Lagerbehälter für Ammoniak
Die hypothetische Brandlast soll zu der zulässigen Werkstofftemperatur von 260 °C am Lagerbehälter führen (s.a. Erläuterung in Beispiel 1).
| Einstelldruck des Sicherheitsventiles: | p = 15,4 bar |
| Verdampfungsenthalpie von Ammoniak bei 42 °C: | r = 1091 kJ/kg |
| Länge des Behälters: | l = 6,0 m |
| Durchmesser des Behälters: | d = 1,5 m |
Aus der Gleichung bzw. dem Diagramm ergibt sich bei 260 °C
(m' ⋅ r) / a = 9,71,
daraus folgt die über das Sicherheitsventil abzuführende Menge mit
| m' | = 9,71⋅ A/r = 9,71⋅ 6/1091 |
| = 0,08 kg/sec | |
| = 288 kg/h |
| Geometrische Darstellung der Bereiche mit möglicher Gesundheitsgefährdung nach Abschnitten 5.2.3.2.1 und 5.2.3.2.4 | Anlage 7 zu TRB 610 |
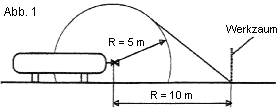 |
 |
 |
| Bestimmung der erforderlichen Wassermenge für eine Wasserberieselung oder Wasserbeflutung für ungestörte Oberflächen nach Abschnitt 3.2.3.3.5. | Anlage 8 zu TRB 610 |
Die Diagramme
Diagramm 1a: Ermittlung der Berieselungsstromdichte Diagramm 1b: Ermittlung der Beflutungsstromdichte Diagramm 2a: Ermittlung der Berieselungsdichte Γ Diagramm 2b: Ermittlung der Beflutungsdichte Γ Diagramm 3: Ermittlung der absorbierten Wärmestromdichte abs
wurden nach folgenden Beziehungen ermittelt:
a Unterfeuerung (Full engulfment)
Die erforderlichen Berieselungs-/Beflutungsstromdichten sind in Abhängigkeit vom Behältervolumen für Kugelbehälter und stehende bzw. liegende zylindrische Behälter in den Diagrammen 1a und 1b dargestellt; die dazugehörigen Berieselungs-/Beflutungsdichten ergeben sich aus den Diagrammen 2a und 2b.
Die Diagramme wurden nach folgenden Beziehungen ermittelt:
 =K1 ⋅
=K1 ⋅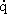 abs+ K2 ⋅ F ⋅ U/A
abs+ K2 ⋅ F ⋅ U/A
mit
K1= 1/cp ⋅ (θ2 - θ1) + r ( 1a)K2 = Γmin ⋅ r ⋅ K1
Γmin = 292 kg / (m ⋅ h)
bzw.
Γ = ⋅ A/U ( 1b)
⋅ A/U ( 1b)
B Unterfeuerung
Bei der Unterfeuerung erfolgt die Erwärmung eines Behälters durch eine Flamme unterhalb des Behälters im Gegensatz zu dem full engulfment, bei dem der gesamte Behälter in Flammen eingehüllt ist.
Von dem von einer Flamme abgegebenen Wärmestrom F gelangt nur der Anteil
F gelangt nur der Anteil abs auf die Behälteroberfläche und wird dort von dem Kühlwasser absorbiert. Es gilt:
abs auf die Behälteroberfläche und wird dort von dem Kühlwasser absorbiert. Es gilt:
 abs = ØBF ⋅
abs = ØBF ⋅ F (2)
F (2)
mit ØBF Einstrahlzeit (geometrische Größe).
Die Berechnung der erforderlichen Kühlwassermassenströme mit Hilfe der Einstrahlzahl und unter entsprechender Anwendung des Rechenganges für full engulfment ist sehr aufwendig, im Einzelfall jedoch möglich.
Im folgenden werden für zwei Sonderfälle vereinfachte Berechnungsmöglichkeiten vorgestellt:
Dann ist K1 in den Gleichungen ( 1a) und ( 1b) zu ersetzen durch K1´ wobei gilt:
K1´ = K1 ⋅ A´/A
mit A´ Anteil der Behälteroberfläche A, der in Flammen steht.
Der Lösungsweg ist analog dem für den Nachbarschaftsbrand anzuwenden: (Modell: Flamme = Kreisscheibe).
C Nachbarschaftsbrand
Wie bei der Unterfeuerung gelangt auch beim Nachbarschaftsbrand nur ein Teil des von einer Flamme abgegebenen Wärmestromes auf die Behälteroberfläche, Gleichung (2) findet ebenso Anwendung.
Mit Hilfe folgenden Modells (Flamme = Kreisscheibe) kann die größte, auf der Behälteroberfläche absorbierte Wärmestromdichte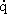 abs berechnet werden:
abs berechnet werden:
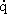 abs=
abs=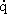 F/(1 + πa2/AF) (3)
F/(1 + πa2/AF) (3)
mit
a Abstand Flamme-Behälter
AF Flammengröße.
Die auf der Behälteroberfläche auftreffende Wärmestromdichte ist im Diagramm 3 über der Entfernung aufgetragen; man erkennt beispielsweise bei einer Flammengröße von 10 m2, dass sich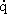 abs, von 100 kW/m2 (Abstand 0) schon in einer Entfernung von 5 m auf 11 kW/m2 verringert.
abs, von 100 kW/m2 (Abstand 0) schon in einer Entfernung von 5 m auf 11 kW/m2 verringert.
Setzt man den so errechneten Wert in die Gleichungen (1a) und (1b) ein, so sind  bzw. Γ bekannt.
bzw. Γ bekannt.
Berieselung:
Kühlung eines Behälters mit Wasser. Das Wasser wird gleichmäßig mit Hilfe eines Düsensystems auf die zu kühlende Oberfläche aufgebracht.
Beflutung:
Kühlung eines Behälters mit Wasser. Das Wasser wird zentral über einen im oberen Behälterbereich angeordneten Zahnkranz aufgebracht. Das überlaufende Wasser läuft als gleichmäßiger Wasserfilm an der Behälteroberfläche ab.
Berieselungs- (Beflutungs-) stromdichte :
:
Wassermassenstrom zur Berieselung (Beflutung), bezogen auf die zu kühlende Behälteroberfläche,
in kg/(m2 ⋅ h).
Berieselungs-(Beflutungs-)stromdichte Γ :
Wassermassenstrom zur Berieselung (Beflutung) bezogen auf den größten horizontalen Behälterumfang,
in kg/(m ⋅ h).
Unterfeuerung
Brandereignis, bei dem in der Behältertasse angesammelte Flüssigkeit abbrennt.
Full engulfment:
Unterfeuerung, bei der der unterfeuerte Behälter vollständig in Flammen eingehüllt ist.
Nachbarschaftsbrand:
Brandereignis außerhalb der Behältertasse.
Wärmestromdichte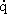 F:
F:
Von einer Flamme abgegebener Wärmestrom, bezogen auf die Flammenoberfläche,
in kW/m2.
Wärmestromdichte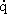 abs
abs
Der Anteil des von der Flamme abgegebenen Wärmestromes, der von der Behälteroberfläche bzw. von dem Kühlwasser, das an seiner Oberfläche abläuft, absorbiert wird, bezogen auf die Behälteroberfläche,
in kW/m2.
| Es bedeuten: | |||
| A | = | Behälteroberfläche | |
| AF | = | Flammengröße | |
| a | = | Abstand Flamme-Behälter | |
| cp | = | spezifische Wärmekapazität von Wasser | |
| F | = | Faktor; (1 für Beflutung, 2 für Berieselung) | |
| Γ | = | Berieselungs- /Beflutungsdichte [kg ⋅ (m-1 ⋅ h-1)]. | |
 |
= | Verdampfungsenthalpie von Wasser | |
| ØBF | = | Einstrahlzahl (geometrische Größe) | |
| θ1 | = | Kühlwassertemperatur = 20 °C | |
| θ2 | = | Siedetemperatur von Wasser = 100 °C | |
| m | = | Berieselungs-/Beflutungsstromdichte [kg ⋅ (m-2 ⋅ h-1)] | |
 abs abs |
= | absorbierter Wärmestrom | |
 F F |
= | abgegebener Wärmestrom der Flamme | |
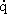 abs abs |
= | absorbierte Wärmedichte | |
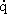 F F |
= | Wärmestromdichte der Flamme; z.B. für Dieselkraftstoff 100 kW ⋅ m-2 | |
| U | = | größter horizontaler Behälterumfang | |
 |
ENDE |  |
(Stand: 08.12.2018)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: ab 105.- € netto
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion