umwelt-online-Demo: Archivdatei - DIN 1045-1 - Tragwerke aus Beton, Stahlbeton und Spannbeton

umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (5)

8.7.2 Vorspannkraft

(1) Die am Spannglied aufgebrachte HöchstkraftP₀, d. h. die Kraft am Spannende während des Spannvorgangs, darf den kleineren der folgenden Werte nicht überschreiten:

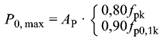(48)

(2) Ein Überspannen ist unter der Voraussetzung zulässig, dass die Spannpresse eine Messunsicherheit der aufgebrachten Spannkraft von ± 5 %, bezogen auf den Endwert der Vorspannkraft, sicherstellt; unter dieser Voraussetzung darf während des Spannvorgangs die höchste PressenkraftP_{0, max} auf 0,95f_{p0, 1k} *A_p gesteigert werden. ⁸)

(3) Der Mittelwert der VorspannkraftP_m0 zum Zeitpunktt =t₀ unmittelbar nach Absetzen der Pressenkraft auf den Anker (Vorspannung im nachträglichen oder ohne Verbund) oder nach dem Lösen der Verankerung (Vorspannung im sofortigen Verbund) darf den kleineren der folgenden Werte an keiner Stelle überschreiten:

(49)

(4) In Abhängigkeit von der Art der Vorspannung sind bei der Berechnung vonP_m0 folgende Einflüsse zu berücksichtigen:

die elastische Verformung,
die Kurzzeitrelaxation des Spannstahls,
der Reibungsverlust,
der Verankerungsschlupf.

(5) Bei internen Spanngliedern ohne Verbund braucht ein Temperaturunterschied zwischen dem Spannglied und dem benachbarten Beton in der Regel nicht berücksichtigt zu werden.

(6) Der Mittelwert der VorspannkraftP_mt zum Zeitpunktt >t₀ ist in Abhängigkeit von der Vorspannart zu bestimmen. Zusätzlich zu den in Absatz (4) genannten Einflüssen sind dabei die Spannkraftverluste infolge Kriechens und Schwindens des Betons und der Langzeitrelaxation des Spannstahls mit den Erwartungswerten zu berücksichtigen.

(7) Beim Vorspannen mit Spanngliedern im nachträglichen oder ohne Verbund muss der Beton zum Zeitpunktt_j des Vorspannens eine Mindestdruckfestigkeitf_cmj aufweisen. Die Mindestdruckfestigkeiten für Teilvorspannen und endgültiges Vorspannen sind in Tabelle 6 in Abhängigkeit von der für das Spannverfahren nach der allgemeinen bauaufsichtlichen Zulassung erforderlichen Mindestfestigkeitsklasse des Betons angegeben. Beim Teilvorspannen gelten die Werte der Tabelle 6, Spalte 1, wobei die Spannkraft in jedem einzelnen Spannglied 30 % des in der allgemeinen bauaufsichtlichen Zulassung angegebenen zulässigen Wertes nicht übersteigen darf. Liegt die durch Erhärtungsprüfungen nachzuweisende Betondruckfestigkeit zum Vorspannzeitpunkt zwischen den Werten nach Tabelle 6, Spalten 1 und 2, darf die Spannkraft entsprechend linear zwischen 30 % und 100 % interpoliert werden.

(8) Die tatsächlichen Werte der Spannkraftverluste während des Spannens sind durch Messung der Spannkraft und des zugehörigen Dehnwegs zu überprüfen.

Tabelle 6 - Mindestbetondruckfestigkeitf_cmj beim Vorspannen mit Spanngliedern im nachträglichen oder ohne Verbund zum Zeitpunktt =t_j

Zeile	Spalte	1	2
	Festigkeitsklasse^a	Festigkeitenf_cmj in N/mmβ^b
	Festigkeitsklasse^a	Teilvorspannen	endgültiges Vorspannen
1	C25/30	13	26
2	C30/37	15	30
3	C35/45	17	34
4	C40/50	19	38
5	C45/55	21	42
6	C50/60	23	46
7	C55/67	25	50
8	C60/75	27	54
9	C70/85	31	62
10	C80/95	35	70
11	C90/105	39	78
12	C100/115	43	86

^a	Gilt sinngemäß auch für Leichtbeton der Festigkeitsklassen LC25/28 bis LC60/66.
^b	Es gilt der Mittelwert der Zylinderdruckfestigkeit (bei Verwendung von Würfeln ist im Verhältnis der Festigkeitsklassen umzurechnen).

8.7.3 Spannkraftverluste

(1) Für die Berechnung der Spannkraftverluste nach 8.7.2 (4) und (6) gelten die in diesem Abschnitt angegebenen Festlegungen.

(2) Die Regelungen der allgemeinen bauaufsichtlichen Zulassung für das jeweilige Spannverfahren sind einzuhalten.

(3) Der Spannkraftverlust aus Reibung ΔP_µ(x) in Spanngliedern darf abgeschätzt werden aus:

ΔP_µ(x) =P₀ * (1 -e^{- µ * (}^Θ^{+k *x)})

(50)

Dabei ist

Θ	die Summe der planmäßigen, horizontalen und vertikalen Umlenkwinkel über die Längex (unabhängig von Richtung und Vorzeichen)
k	der ungewollte Umlenkwinkel (je Längeneinheit); abhängig von der Art des Spannglieds
µ	Reibungsbeiwert zwischen Spannglied und Hüllrohr, hängt von der Oberflächenbeschaffenheit der Spannglieder und der Hüllrohre, der Längenänderung des Spannglieds und der Spannstahloberfläche ab

(4) Bei extern geführten Spanngliedern, die aus parallelen Drähten oder Litzen bestehen, darf der Spannkraftverlust infolge ungewollter Umlenkwinkel vernachlässigt werden.

(5) Bei Spanngliedern ohne Verbund braucht die Reibung nur bei der Ermittlung der wirksamen mittleren VorspannkraftP_mt und der Ermittlung der daraus resultierenden Momente infolge der Eintragung der Vorspannkraft berücksichtigt zu werden.

(6) Zeitabhängige Verluste zum Zeitpunktt = ∞ dürfen für einsträngige Vorspannung im Verbund berechnet werden aus:

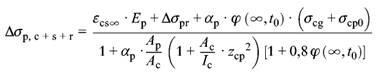(51)

Dabei ist

Δσ_{p, c + s + r}	die Spannungsänderung im Spannstahl aus Kriechen und Schwinden des Betons und Relaxation des Spannstahls an der Stelle x bis zum Zeitpunktt =t_.
ε_cs∞	das Endschwindmaß nach 9.1.4
α_p	das Verhältnis (E_p/E_cm) der Elastizitätsmoduln des Spannstahls und des Betons
E_p	der Elastizitätsmodul des Spannstahls nach 9.3
E_cm	der mittlere Elastizitätsmodul des Betons nach Tabelle 9 oder Tabelle 10
Δσ_pr	die Spannungsänderung im Spannstahl an der Stellex infolge Relaxation (Δσ_pr < 0). Diese darf mit den Angaben der allgemeinen bauaufsichtlichen Zulassung des Spannstahls für das Verhältnis der Ausgangsspannung zur charakteristischen Zugfestigkeit (σ_p0/f_pk) bestimmt werden; mit einer Ausgangsspannung vonσ_p0 =σ_pg0 - 0,3 Δσ_{p, c + s + r}, wobeiσ_pg0 die anfängliche Spannstahlspannung aus der Vorspannung und den ständigen Einwirkungen ist. Zur Vereinfachung darf auf der sicheren Seite liegendσ_p0 =σ_pg0 gesetzt werden; für übliche Hochbauten darfσ_p0 zu 0,95σ_pg0 angenommen werden. Ansonsten ist Δσ_pr in Gleichung (51) iterativ zu ermitteln.
Φ(∞, t₀)	die Endkriechzahl des Betons nach 9.1.4
σ_cg	die Betonspannung in Höhe der Spannglieder unter der quasi-ständigen Einwirkungskombination
σ_cp0	der Anfangswert der Betonspannung in Höhe der Spannglieder infolge Vorspannung
I_c	das Flächenmoment 2. Grades des Betonquerschnitts
z_cp	der Abstand zwischen dem Schwerpunkt des Betonquerschnitts und den Spanngliedern

Druckspannungen sind in Gleichung (51) negativ einzusetzen

(7) Für die Ermittlung des zeitabhängigen Spannkraftverlustes in einem Spannglied ohne Verbund darf Gleichung (51) angewendet werden, wenn für Schwinden und Kriechen die über die Spanngliedlänge gemittelten Betondehnungen

bei externen Spanngliedern im Bereich gerader Abschnitte zwischen den idealisierten Knickpunkten oder Verankerungsstellen und
bei internen Spanngliedern entlang der Gesamtlänge des Spannglieds

angesetzt werden.

8.7.4 Grenzzustand der Gebrauchstauglichkeit

(1) Mögliche Streuungen der Vorspannkraft sind zu berücksichtigen. Dazu sind zwei charakteristische Werte der Vorspannkraft anzusetzen:

P_{k, sup} =r_sup *P_mt	(52)
P_{k, inf} =r_inf *P_mt	(53)

Dabei ist

P_{k, sup}	der obere charakteristische Wert der Vorspannkraft
P_{k, inf}	der untere charakteristische Wert der Vorspannkraft
P_mt	der Mittelwert der Vorspannkraft

(2) Für die Beiwerter_sup undr_inf dürfen im Allgemeinen die folgenden Werte angenommen werden:

r_sup = 1,05 undr_inf = 0,95 bei Vorspannung im sofortigem oder ohne Verbund

r_sup = 1,10 undr_inf = 0,90 bei Vorspannung im nachträglichem Verbund

8.7.5 Grenzzustand der Tragfähigkeit

(1) Der Bemessungswert der VorspannkraftP_d =γ_P *P_mt darf im Allgemeinen mitγ_P = 1,0 ermittelt werden.

(2) Mögliche Streuungen der Vorspannkraft dürfen bei den Nachweisen im Grenzzustand der Tragfähigkeit im Allgemeinen vernachlässigt werden.

(3) Wird bei Spanngliedern ohne Verbund der Spannungszuwachs im Spannstahl berücksichtigt, ist der charakteristische Wert Δσ_pk des Spannungszuwachses im Spannstahl mit den Mittelwerten der Baustoffeigenschaften zu bestimmen. Zur Ermittlung des Bemessungswertes Δσ_pd =γ_P * Δσ_pk gilt bei linearelastischer Schnittgrößenermittlung:

γ_P = 1,0

Bei einem nichtlinearen Verfahren der Schnittgrößenermittlung ist ein oberer oder ein unterer Grenzwert fürγ_P anzusetzen, wobei die Rissbildung oder die Fugenöffnung (Segmentbauweise) zu berücksichtigen ist:

γ_{P, sup}= 1,2 und

γ_{P, inf} = 0,83

(der jeweils ungünstigere Wert ist anzusetzen)

8.7.6 Verankerungsbereiche bei Spanngliedern im sofortigen Verbund

(1) Für Vorspannung im sofortigen Verbund ist die Verwendung von glatten Drähten nicht zulässig.

(2) Bei Spanngliedern im sofortigen Verbund ist zu unterscheiden zwischen:

der Übertragungslängel_bp, über die die SpannkraftP₀ eines Spanngliedes im sofortigen Verbund voll auf den Beton übertragen wird,
der Eintragungslängel_p,eff, innerhalb der die Betonspannung in eine lineare Verteilung über den Betonquerschnitt übergeht,
der Verankerungslängel_ba, innerhalb der die maximale Spanngliedkraft im Grenzzustand der Tragfähigkeit vollständig verankert ist.

(3) Es darf angenommen werden, dass die Vorspannung durch eine konstante Verbundspannungf_bp in den Beton eingetragen wird. Die Übertragungslängel_bp darf wie folgt ermittelt werden:

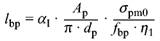(54)

Dabei ist

α_l	= 1,0 bei stufenweisem Eintragen der Vorspannung
	= 1,25 bei schlagartigem Eintragen der Vorspannung
A_p	der Nennquerschnitt der Litze oder des Drahts
d_p	der Nenndurchmesser der Litze oder des Drahts
σ_pm0	die Spannung im Spannstahl nach der Spannkraftübertragung auf den Beton
η₁	= 1,0 für Normalbeton; für Leichtbeton nach Tabelle 10

(4) Für normale (nicht verdichtete) Litzen mit einer QuerschnittsflächeA_p< 100 mm² und für profilierte Drähte mit einem Durchmesser< 8 mm, die nach den Angaben in 8.7.2 vorgespannt sind, dürfen die in Tabelle 7 angegebenen Werte für die Verbundspannungf_bp angenommen werden. Maßgebend ist die Betondruckfestigkeit zum Zeitpunkt der Spannkraftübertragung auf den Beton. Bei Verwendung von gerippten Drähten mit Durchmessern< 12 mm sollten die Werte für die Verbundspannungf_bp aus Versuchsergebnissen abgeleitet werden. Als Näherung dürfen die Werte der Tabelle 7 herangezogen werden.

Bei mäßigen Verbundbedingungen (siehe 12.4) sind die Werte der Verbundspannung in Tabelle 7 mit dem Faktor 0, 7 abzumindern.

(5) Es darf angenommen werden, dass die auf den Beton übertragene Vorspannkraft innerhalb der Übertragungslängel_bp linear vom Bauteilende her zunimmt.

(6) Der Bemessungswert der Übertragungslängel_bpd ist mit 0,8l_bp oder 1,2l_bp anzunehmen; es gilt der ungünstigere Wert für die betrachtete Wirkung.

(7) Für die Spannungsermittlung im Eintragungsbereich darf am Ende der Eintragungslängel_{p, eff} eine lineare Verteilung der Betonspannungen über den Querschnitt angenommen werden.

(8) Die Eintragungslängel_{p, eff} ff darf für Rechteckquerschnitte mit Spanngliedern nahe der Unterseite des Querschnitts wie folgt bestimmt werden:

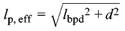(55)

Für andere Querschnittsformen sollten die Eintragungslänge und die jeweilige örtliche Spannungsverteilung in Anlehnung an die Elastizitätstheorie festgelegt werden.

(9) In biegebeanspruchten Bauteilen wird die Verankerung der Vorspannung durch Rissbildung entscheidend beeinflusst. Der Verankerungsbereich darf als ungerissen angesehen werden, wenn im Grenzzustand der Tragfähigkeit die Betonzugspannungen unter Berücksichtigung der maßgebenden Vorspannkraft die Betonzugfestigkeitf_{ctk; 0,05} nicht überschreiten. In diesem Fall darf die Verankerung innerhalb der Längel_bpd ohne weiteren Nachweis als gegeben angesehen werden.

Tabelle 7 - Verbundspannungf_bp in der Übertragungslänge von Litzen und Drähten im sofortigen Verbund in Abhängigkeit von der Betondruckfestigkeit zum Zeitpunkt der Spannkraftübertragung

Zeile	Spalte	1	2
	Tatsächliche Betondruckfestigkeit bei der Spannkraftübertragungf_cmj in N/mm^{2 a b}	Verbundsspannungf_bp in N/mm²
		Litzen und profilierte Drähte	gerippte Drähte
1	25	2,9	3,8
2	30	3,3	4,3
3	35	3,7	4,8
4	40	4,0	5,2
5	45	4,3	5,6
6	50	4,6	6,0
7	60	5,0	6,5
8	70	5,3	6,9
9	80	5,5	7,2
10	290	5,7	7,4

^a	Zwischenwerte sind linear zu interpolieren.
^b	Es gilt der Mittelwert der Zylinderdruckfestigkeit (bei Verwendung von Würfeln ist im Verhältnis der Festigkeitsklassen umzurechnen).

(10) Überschreiten die Betonzugspannungen den Wertf_{ctk; 0,05}, ist nachzuweisen, dass die vorhandene Zugkraftlinie die Zugkraftdeckungslinie aus der Zugkraft von Spannstahl und Betonstahl nicht überschreitet (vgl. Bild 66). Die Zugkraft im Spannstahl ist nach Bild 17 zu ermitteln. Außerhalb der Übertragungslängel_bpd bzw. . nach dem ersten Riss (x>l_r) sind dabei wegen der schlechteren Verbundbedingungen die Werte der Verbundspannungen nach Tabelle 7 abzumindern. Die Längel_ba darf wie folgt ermittelt werden.

a) bei Rissbildung außerhalbl_bpd (siehe Bild 17a)):

(56)

b) bei Rissbildung innerhalbl_bpd (siehe Bild 17b)):

(57)

mit

η_p = 0,5	für Litzen und profilierte Drähte bzw. .
η_p = 0,7	für gerippte Drähte

Bild 17 - Verlauf der Spannstahlspannungen im Verankerungsbereich von Spanngliedern im sofortigen Verbund

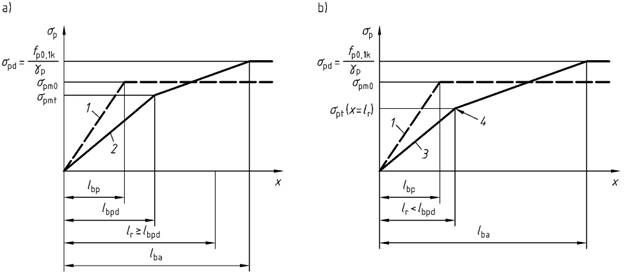
Legende

bei der Spannkrafteinleitung (1), im Grenzzustand der Tragfähigkeit ohne Rissbildung in der Übertragungslänge (2)
mit Rissbildung in der Übertragungslänge (3), (4) Stelle des ersten Biegerisses

(11) Die in der Entfernungx vom Bauteilende zu verankerndeF_Ed(x) beträgt:

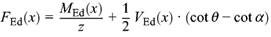(58)

Dabei ist

M_Ed(x)	der Bemessungswert des aufzunehmenden Biegemoments an der Stellex
z	der innere Hebelarm nach 10.3.4
V_Ed(x)	der Bemessungswert der zugehörigen aufzunehmenden Querkraft an der Stellex
θ	der Winkel zwischen den Betondruckstreben und der Bauteillängsachse nach 10.3.4; für Bauteile ohne Querkraftbewehrung gilt cotθ = 3,0 und cotα = 0
α	der Winkel zwischen der Querkraftbewehrung und der Bauteilachse nach 10.3.4

Bei der Ermittlung der vom Spannstahl aufzunehmenden Verankerungskraft ist die Rissbildung zu berücksichtigen (siehe Bild 17).

8.7.7 Verankerungsbereiche bei Spanngliedern mit nachträglichem oder ohne Verbund

Die im Verankerungsbereich erforderliche Spaltzug- und Zusatzbewehrung ist der allgemeinen bauaufsichtlichen Zulassung für das Spannverfahren zu entnehmen. Der Nachweis der Kraftaufnahme und -weiterleitung im Tragwerk ist mit einem geeigneten Verfahren (z.B. mit einem Stabwerkmodell nach 10.6) zu führen.

9 Baustoffe

9.1 Beton

9.1.1 Allgemeines

(1) Dieser Abschnitt gilt für Beton (Normal- und Leichtbeton) nach DIN EN 206-1 und DIN 1045-2.

(2) Die in diesem Abschnitt angegebenen Festigkeits- und Formänderungskennwerte gelten, sofern für Leichtbeton nicht ausdrücklich festgelegt, für Normalbeton und Leichtbeton.

(3) Die Festigkeitsklassen für Normalbeton werden durch das vorangestellte Symbol C, für Leichtbeton durch das vorangestellte Symbol LC gekennzeichnet. Die erste Zahl bezeichnet die Zylinderdruckfestigkeit und die zweite Zahl die Würfeldruckfestigkeit (z.B. C20/25).

(4) Leichtbeton wird entsprechend seiner Trockenrohdichte in Rohdichteklassen nach DIN 1045-2 sowie DIN EN 206-1 eingeteilt. Der Rechenwertρ der Trockenrohdichte und der charakteristische Wert der Wichte des Betons sind Tabelle 8 zu entnehmen.

9.1.2 Festigkeiten

(1) Den Festigkeitsklassen dieser Norm liegt die charakteristische Zylinderdruckfestigkeitf_ck nach 28 Tagen zugrunde (siehe Tabelle 9 und Tabelle 10). Für ihre Definition gelten DIN 1045-2 und DIN EN 206-1.

(2) In bestimmten Fällen (z.B. beim Vorspannen) kann es erforderlich sein, die Druckfestigkeit zu einem früheren oder späteren Zeitpunkt als nach 28 Tagen oder für besondere Lagerungsbedingungen (z.B. Wärmebehandlung) zu bestimmen.

(3) Die Zugfestigkeitf_ct bezieht sich im Rahmen dieser Norm auf die erreichbare Höchstspannung unter einachsiger zentrischer Zugbeanspruchung.

Tabelle 8 - Rohdichteklasse, Rechenwertρ der Trockenrohdichte und charakteristischer Wert der Wichte von Leichtbeton

Zeile	Spalte		1	2	3	4	5	6
			Rohdichteklasse
			D1,0	D1,2	D1,4	D1,6	D1,8	D2,0
1	RechenwertÁ der Trockenrohdichte zur Bestimmung der Baustoffeigenschaften in kg/m³		801-1000	1001-1200	1201-1400	1401-1600	1601-1800	1801-2000
2	charakteristischer Wert der Wichte zur Lastermittlung in kg/m³	unbewehrter Leichtbeton	1050	1250	1450	1650	1850	2050
2		bewehrter Leichbeton	1150	1350	1550	1750	1950	2150

(4) Die zentrische Zugfestigkeitf_ctdarf aus der Spaltzugfestigkeitf_{ct, sp} näherungsweise berechnet werden zu:

f_ct = 0,9f_{ct, sp}

(59)

9.1.3 Elastische Verformungseigenschaften

(1) Die elastischen Verformungen des Betons hängen in hohem Maße von seiner Zusammensetzung (vor allem von der Gesteinskörnung) ab. Die im Folgenden gegebenen Angaben stellen deshalb lediglich Richtwerte dar. Sie sind dann gesondert zu ermitteln, wenn das Tragwerk empfindlich auf entsprechende Abweichungen reagiert.

(2) Richtwerte für die Elastizitätsmoduln (Sekantenmoduln)E_cm undE_lcm dürfen Tabelle 9 und Tabelle 10 entnommen werden.

(3) Die Querdehnzahl für die elastische Dehnung darf näherungsweise zu Null angenommen werden.

(4) Die lineare Wärmedehnzahl darf für Normalbeton im Allgemeinen gleich 10 * 10^-6 K^-1 und für Leichtbeton im Allgemeinen gleich 8 * 10^-6 K^-1 gesetzt werden.

(5) Der Unterschied zwischen den Wärmedehnzahlen von Stahl und Leichtbeton darf bei der Bemessung vernachlässigt werden.

9.1.4 Kriechen und Schwinden

(1) Kriechen und Schwinden des Betons hängen im Wesentlichen von der Feuchte der Umgebung, den Abmessungen des Bauteils und der Zusammensetzung des Betons ab. Das Kriechen wird des Weiteren deutlich vom Reifegrad des Betons beim erstmaligen Aufbringen der Last sowie von Dauer und Größe der Belastung beeinflusst. Bei der Ermittlung der KriechzahlΦ(t,t₀)und der Schwinddehnungε_cs sind diese Einflüsse zu berücksichtigen.

(2) Die nach diesem Abschnitt ermittelten EndkriechzahlenΦ(∞,t₀) und Schwinddehnungenε_cs∞ dürfen als zu erwartende Mittelwerte angesehen werden. Die mittleren Variationskoeffizienten für die Vorhersage der EndkriechzahlΦ(∞,t₀) und der Schwinddehnungε_cs∞ liegen bei etwa 30 %. Für gegenüber Kriechen und Schwinden empfindliche Tragwerke sollte die mögliche Streuung dieser Werte berücksichtigt werden. Die angegebenen Werte gelten für kriecherzeugende Betondruckspannungen von nicht mehr als 0,45f_ckj; dabei istf_ckj die Zylinderdruckfestigkeit des Betons zum Zeitpunkt des Aufbringens der kriecherzeugenden Spannung.

(3) Wenn die kriecherzeugende Betondruckspannung den Wert 0,45f_ckj überschreitet, muss die nichtlineare Abhängigkeit des Kriechens von der kriecherzeugenden Spannung berücksichtigt werden. Dies gilt insbesondere bei Vorspannung mit sofortigem Verbund.

(4) In den Fällen nach Absatz (3) und für genauere Berechnungen dürfen die Kriechzahlen mit anderen geeigneten Berechnungsverfahren ermittelt werden.

(5) Die nach diesem Abschnitt ermittelten EndkriechzahlenΦ(∞,t₀) und Schwinddehnungenε_cs∞ gelten für Konstruktionsbetone, die nicht länger als 14 Tage feucht nachbehandelt werden und die üblichen Umgebungsbedingungen mit einer mittleren relativen Luftfeuchte zwischen 40 % und 100 % und mittleren Temperaturen zwischen 10 °C und 30°C ausgesetzt sind.

(6) Die Kriechdehnung des Betonsε_cs (∞,t₀) zum Zeitpunktt = ∞ darf bei zeitlich konstanter kriecherzeugender Spannung wie folgt berechnet werden:

(60)

Dabei ist

Φ(∞,t₀)	die Endkriechzahl; diese darf in Abhängigkeit von der relativen Luftfeuchte vereinfachend Bild 18 oder Bild 19 entnommen werden; für mittlere relative Luftfeuchten unter 50 % und zwischen 50 % und 80 % darf linear extrapoliert bzw. . linear interpoliert werden.
E_c0	der Elastizitätsmodul des Betons als Tangente im Ursprung der Spannungs-Dehnungs-Linie nach 28 Tagen. Vereinfachend kannE_c0 = 1,1 Ecm angenommen werden; dabei ist Ecm der mittlere Sekantenmodul des Betons aus Tabelle 9 oder Tabelle 10
σ_c	die zeitlich konstante kriecherzeugende Betonspannung
t₀	das Betonalter bei Belastungsbeginn in Tagen

(7) Für Leichtbeton dürfen, sofern keine Versuchsergebnisse vorliegen, die Werte der EndkriechzahlΦ(∞,t₀) nach Bild 18 oder Bild 19 zugrunde gelegt werden, wenn Sie mit dem Faktorη_E nach Tabelle 10 abgemindert werden. Die so ermittelte Endkriechzahl ist für Betone der Festigkeitsklassen LC12/13 und LC16/18 zusätzlich mit dem Faktorη₂ = 1,3 zu multiplizieren.

(8) Zur Berechnung der Kriechzahl zu einem beliebigen Zeitpunkt und bei zeitlich nicht konstanter Betonspannung siehe DAfStb-Heft 525.

Bild 18 - EndkriechzahlΦ( ∞ ,t₀) für Normalbeton und trockene Umgebungsbedingungen (trockene Innenräume, relative Luftfeuchte = 50 %)

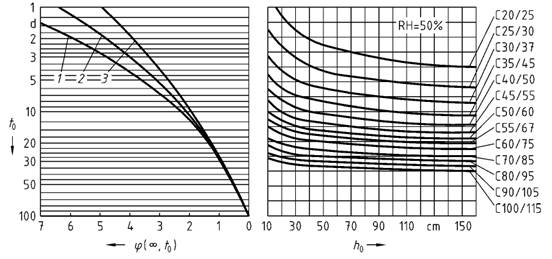
Legende

1	Festigkeitsklasse des Zements 32,5^*)
2	Festigkeitsklasse des Zements 32,5R; 42,5^*)
3	Festigkeitsklasse des Zements 42,5R; 52,5^*)

^*) Weitere Beispiele für die Zuordnung der Zementarten siehe Heft 525

Dabei ist

h₀	die wirksame Querschnittsdicke
	= 2A_c/u
A_c	die Querschnittsfläche
u	der Umfang des Querschnitts (bei Kastenträgern einschließlich 50 % des inneren Umfangs)

Bild 19 - EndkriechzahlΦ(∞ ,t₀) für Normalbeton und feuchte Umgebungsbedingungen (Außenluft, relative Luftfeuchte = 80 %)

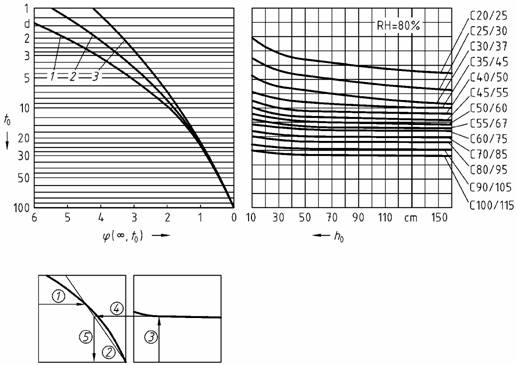
Legende

1	Festigkeitsklasse des Zements 32,5^*)
2	Festigkeitsklasse des Zements 32,5R; 42,5^*)
3	Festigkeitsklasse des Zements 42,5R; 52,5^*)

^*) Weitere Beispiele für die Zuordnung der Zementarten siehe Heft 525

Dabei ist

h₀	die wirksame Querschnittsdicke
	= 2A_c/u
A_c	die Querschnittsfläche
u	der Umfang des Querschnitts (bei Kastenträgern einschließlich 50 % des inneren Umfangs)

(9) Die Schwinddehnung des Betons setzt sich aus den Anteilen Schrumpfdehnung und Trocknungsschwinddehnung zusammen und darf für den Zeitpunktt = ∞ wie folgt berechnet werden:

ε_cs∞ =ε_cas∞ +ε_cds∞

(61)

Dabei ist

ε_cs∞	die Schwinddehnung des Betons zum Zeitpunktt = ∞
ε_cas∞	die Schrumpfdehnung zum Zeitpunktt = ∞ nach Bild 20
ε_cds∞	die Trocknungsschwinddehnung zum Zeitpunktt = ∞ nach Bild 21

(10) Für Leichtbeton darf, , sofern keine Versuchsergebnisse vorliegen, die Schwinddehnungε_cds∞ nach Gleichung (61) zugrunde gelegt werden. Die Werte sind dabei für Betone der Festigkeitsklassen LC12/13 und LC16/18 mit dem Faktorη₃ = 1,5 und für Betone der Festigkeitsklassen ab LC20/22 mit dem Faktorη₃ = 1,2 zu multiplizieren.

(11) Zur Berechnung der Schwinddehnung zu einem beliebigen Zeitpunkt siehe DAfStb-Heft 525.

Bild 20 - Schrumpfdehnungε_cas∞ zum Zeitpunktt = ∞ für Normalbeton

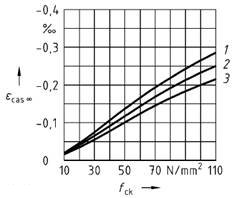
Legende

1	Festigkeitsklasse des Zements 32,5^*)
2	Festigkeitsklasse des Zements 32,5R; 42,5^*)
3	Festigkeitsklasse des Zements 42,5R; 52,5^*)

^*) Weitere Beispiele für die Zuordnung der Zementarten siehe Heft 525

Dabei ist

h₀	die wirksame Querschnittsdicke
	= 2A_c/u
A_c	die Querschnittsfläche
u	der Umfang des Querschnitts (bei Kastenträgern einschließlich 50 % des inneren Umfangs)

Bild 21 - Trocknungsschwinddehnungε_cds∞ zum Zeitpunktt = ∞ für Normalbeton

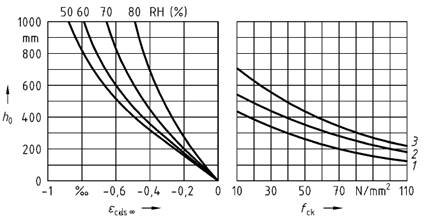
Legende

1	Festigkeitsklasse des Zements 32,5^*)
2	Festigkeitsklasse des Zements 32,5R; 42,5^*)
3	Festigkeitsklasse des Zements 42,5R; 52,5^*)

^*) Weitere Beispiele für die Zuordnung der Zementarten siehe Heft 525

Dabei ist

h₀	die wirksame Querschnittsdicke
	= 2A_c/u
A_c	die Querschnittsfläche
u	der Umfang des Querschnitts (bei Kastenträgern einschließlich 50 % des inneren Umfangs)

9.1.5 Spannungs-Dehnungs-Linie für nichtlineare Verfahren der Schnittgrößenermittlung und für Verformungsberechnungen

(1) Für nichtlineare Verfahren der Schnittgrößenermittlung und für Verformungsberechnungen ist die Spannungs-Dehnungs-Linie nach Bild 22 zu verwenden. Die Spannungs-Dehnungs-Linie wird für kurzzeitig wirkende Beanspruchungen und einaxiale Spannungszustände durch Gleichung (62) beschrieben:

(62)

mit

η =ε_c /ε_c1	(63)
k = - 1,1E_cm *ε_c1 /f_c	(64)

Dabei ist

ε_c1	die Dehnung bei Erreichen des Höchstwerts der Betondruckspannung nach Tabelle 9 oder Tabelle 10
E_cm	der mittlere Elastizitätsmodul nach Tabelle 9 oder Tabelle 10
f_c	der Höchstwert der ertragenen Betondruckspannung; bei nichtlinearen Verfahren der Schnittgrößenermittlung darf fürf_c der Rechenwertf_cR nach 8.5.1 angenommen werden; bei Verformungsberechnungenf_cm

Gleichung (62) ist für 0>ε_c>ε_c1u gültig, wobeiε_c1u die Bruchdehnung bei Erreichen der Festigkeitsgrenze nach Tabelle 9 oder Tabelle 10 ist.

(2) Andere idealisierte Spannungs-Dehnungs-Linien dürfen angewendet werden, wenn sie dem in Absatz (1) beschriebenen Ansatz gleichwertig sind.

weiter .

umwelt-online - Demo-Version

(Stand: 01.03.2019)

Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: 90.- € netto (Grundlizenz)

(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)

Preise & Bestellung

Die Zugangskennung wird kurzfristig übermittelt

? Fragen ?
Abonnentenzugang/Volltextversion