

umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (6)
 |
zurück |  |
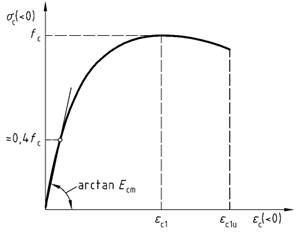
Bild 22 - Spannungs-Dehnungs-Linie für die Schnittgrößenermittlung mit nichtlinearen Verfahren und für Verformungsberechnungen
9.1.6 Spannungs-Dehnungs-Linie für die Querschnittsbemessung
(1) Für die Querschnittsbemessung ist die Spannungs-Dehnungs-Linie nach Bild 23 zu verwenden. Die Spannungs-Dehnungs-Linie wird durch die Gleichungen (65) und (66) beschrieben:
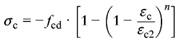 |
für 0>εc>εc2 | (65) |
| σc = -fcd | fürεc2>εc>εc2u | (66) |
Dabei ist
| n | der Exponent der Parabel |
| εc2 | die Dehnung beim Erreichen der Festigkeitsgrenze |
| εc2u | die maximale Dehnung |
Die Werte sind Tabelle 9 oder Tabelle 10 zu entnehmen.
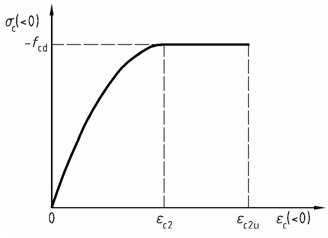
Bild 23 - Parabel-Rechteck-Diagramm
(2) Der Bemessung im Grenzzustand der Tragfähigkeit ist der Wertfcd zugrunde zu legen:
| fcd =α *fck/γc | (67) |
Dabei ist
| γc | der Teilsicherheitsbeiwert für Beton nach Tabelle 2 bzw. bei unbewehrten Bauteilen nach 5.3.3 (8); ab den Festigkeitsklassen C55/67 und LC55/60 istγc mitγc' zu multiplizieren (siehe 5.3.3 (9)). |
| α | der Abminderungsbeiwert zur Berücksichtigung von Langzeitwirkungen auf die Druckfestigkeit sowie zur Umrechnung zwischen Zylinderdruckfestigkeit und einaxialer Druckfestigkeit des Betons. Der Beiwertα ist für Normalbeton mit 0,85 anzunehmen. In begründeten Fällen (z.B. Kurzzeitbelastung) dürfen auch höhere Werte fürα (mitα< 1) angesetzt werden. Für Leichtbeton ist der Wertα nach 9.1.6 (4) zu wählen. |
(3) Andere idealisierte Spannungs-Dehnungs-Linien sind zulässig, sofern sie dem Parabel-Rechteck-Diagramm im Hinblick auf die Verteilung der Druckspannungen gleichwertig sind (z.B. das bilineare Diagramm nach Bild 24 mit den Werten nach Tabelle 9 oder Tabelle 10). Wenn die Dehnungsnulllinie im Querschnitt liegt, darf unter den angegebenen Bedingungen auch der Spannungsblock nach Bild 25 als Betonspannungsverteilung angesetzt werden.
Bild 24 - Bilineare Spannungs-Dehnungs-Linie
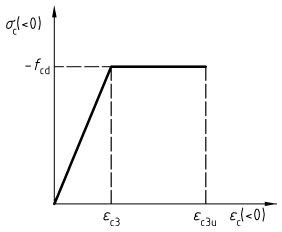
Bild 25 - Spannungsblock
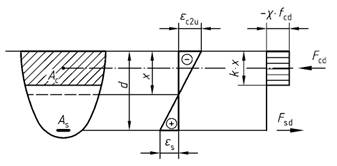
Legende
| χ ≈ 0,95 | fürfck< 50 N/mm2 |
| χ = 1,05 -fck/500 | fürfck > 50 N/mm2 |
| k = 0,80 | fürfck< 50 N/mm2 |
| k = 1,0 -fck/250 | fürfck > 50 N/mm2 |
Anmerkung: Sofern die Querschnittsbreite zum gedrückten Rand hin abnimmt, istfcd zusätzlich mit dem Faktor 0,9 abzumindern.
(4) Für Leichtbeton ist bei Verwendung des Parabel-Rechteck-Diagramms nach Bild 23 oder des Spannungsblocks nach Bild 25α = 0,75, bei Verwendung des bilinearen Diagramms nach Bild 24α = 0,80 zu setzen.
9.1.7 Zusammenstellung der Betonkennwertrte
(1) Die Betonkennwerte sind in Tabelle 9 und Tabelle 10 zusammengestellt.
(2) Der nach 9.1.6 (2) ermittelte Wertfcd ist der Bemessungswert der einaxialen Druckfestigkeit des ungerissenen Betons. Bei Querzugspannungen oder Querrissbildung muss die Verminderung der Druckfestigkeit berücksichtigt werden.
(3) Die Verminderung der Festigkeiten darf vereinfachend mitαc *fcd (αc nach 10.3.4) angenommen werden.
(4) Bei mehraxialen Druckbeanspruchungen dürfen höhere Festigkeiten angesetzt werden.
Tabelle 9 - Festigkeits- und Formänderungskennwerte von Normalbeton
| Zeile | Spalte | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| Kenngröße | Festigkeitsklassen | analytische Beziehung; Erläuterung | ||||||||||||||||
| 1 | fck | 12a | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 70 | 80 | 90 | 100 | N/mm2 | |
| 2 | fck, cube | 15 | 20 | 25 | 30 | 37 | 45 | 50 | 55 | 60 | 67 | 75 | 85 | 95 | 105 | 115 | N/mm2 | |
| 3 | fcm | 20 | 24 | 28 | 33 | 38 | 43 | 48 | 53 | 58 | 63 | 68 | 78 | 88 | 98 | 108 | fcm =fck + 8 | N/mm2 |
| 4 | fctm | 1,6 | 1,9 | 2,2 | 2,6 | 2,9 | 3,2 | 3,5 | 3,8 | 4,1 | 4,2 | 4,4 | 4,6 | 4,8 | 5 | 5,2 | fctm = 0,30fck(2/3)
fctm = 2,12 ln (1 +fcm/10) |
bis C50/60
ab C55/67 |
| 5 | flctk; 0,05 | 1,1 | 1,3 | 1,5 | 1,8 | 2 | 2,2 | 2,5 | 2,7 | 2,9 | 3 | 3,1 | 3,2 | 3,4 | 3,5 | 3,7 | fctk; 0,05 = 0,7fctm | 5 %-Quantil |
| 6 | flctk; 0,95 | 2 | 2,5 | 2,9 | 3,3 | 3,8 | 4,2 | 4,6 | 4,9 | 5,3 | 5,5 | 5,7 | 6 | 6,3 | 6,6 | 6,8 | fctk, 0,95 = 1,3fctm | 95 %-Quantil |
| 7 | Ecmb | ηE *Ecm | 40600 | 42300 | 43800 | 45200 | Ecm = 9500 (fck + 8)1/3 | N/mm2 | ||||||||||
| 8 | εc1 | -1,8 | -1,9 | -2,1 | -2,2 | -2,3 | -2,4 | -2,5 | -2,55 | -2,6 | -2,65 | -2,7 | -2,8 | -2,9 | -2,95 | -3,0 | ino/oo; gilt nur für Bild 22 | |
| 9 | εc1u | -3,5 | -3,4 | -3,3 | -3,2 | -3,1 | -3,0 | -3,0 | ino/oo; gilt nur für Bild 22 | |||||||||
| 10 | n | 2,0 | 2,0 | 1,9 | 1,8 | 1,7 | 1,6 | 1,55 | ||||||||||
| 11 | εc2 | -2,0 | -2,03 | -2,06 | -2,1 | -2,14 | -2,17 | -2,2 | ino/oo; gilt nur für Bild 23 | |||||||||
| 12 | εc2u | -3,5 | -3,1 | -2,7 | -2,5 | -2,4 | -2,3 | -2,2 | ino/oo gilt nur für Bild 23 | |||||||||
| 13 | εc3 | -1,35 | -1,35 | -1,4 | -1,5 | -1,6 | -1,65 | -1,7 | ino/oo; gilt nur für Bild 24 | |||||||||
| 14 | εc3u | -3,5 | -3,1 | -2,7 | -2,5 | -2,4 | -2,3 | -2,2 | ino/oo; gilt nur für Bild 24 | |||||||||
| a | Die Festigkeitsklasse C12/15 darf nur bei vorwiegend ruhenden Einwirkungen verwendet werden. |
| b | Diese Werte stellen den mittleren Elastizitätsmodul als Sekante bei |σc| ≈ 0,4fcm dar. |
Tabelle 10 - Festigkeits- und Formänderungskennwerte von Leichtbeton
| Zeile | Spalte | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Kenngröße | Festigkeitsklassen | analytische Beziehung; Erläuterung | ||||||||||||
| 1 | flck | 12a | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | N/mm2 | |
| 2 | flck, cube | 13 | 18 | 22 | 28 | 33 | 38 | 44 | 50 | 55 | 60 | 66 | N/mm2 | |
| 3 | flcm | 20 | 24 | 28 | 33 | 38 | 43 | 48 | 53 | 58 | 63 | 68 | flcm =flck + 8 | N/mm2 |
| 4 | flctm |
η1 *fctm |
fctm nach Tabelle 9
η1 = 0,40 + 0,60ρ /2200c |
N/mm z | ||||||||||
| 5 | fctk; 0,05 |
η1 *fctk; 0,05 |
fctk; 0,05 nach Tabelle 9 | 5 %-Quantil | ||||||||||
| 6 | fctk; 0,95 |
η1 *fctk; 0,95 |
fctk; 0,95 nach Tabelle 9 | 95 %-Quantil | ||||||||||
| 7 | Elcmb |
ηE *Elcm |
Ecm nach Tabelle 9
ηE = (ρ /2200)2 c |
|||||||||||
| 8 | εlc1u | -k *fkcm/Elcm | k = 1,1 für Leichtbeton mit Leichtsand
k = 1,3 für Leichtbeton mit Natursand |
ino/oo; gilt nur für Bild 22 | ||||||||||
| 9 | εlc1u | εlc1 | ino/oo; gilt nur für Bild 22 | |||||||||||
| 10 | n | 2,0 | 1,9 | |||||||||||
| 11 | εlc2 | -2,0 | -2,03 | -2,06 | ino/oo; gilt nur für Bild 23 | |||||||||
| 12 | εlc2u | - 3,5η1>εc2u | εc2u nach Tabelle 9 | ino/oo; gilt nur für Bild 23 | ||||||||||
| 13 | εk3 | -1,8 | ino/oo; gilt nur für Bild 24 | |||||||||||
| 14 | εlc3u | -3,5η1>εc3u | εc3u nach Tabelle 9 | ino/oo; gilt nur für Bild 24 | ||||||||||
| a | Die Festigkeitsklasse LC12/13 darf nur bei vorwiegend ruhenden Lasten verwendet werden. |
| b | Diese Werte stellen den mittleren Elastizitätsmodul als Sekante bei |σc| ≈ 0,4flcm dar. |
| c | mitρ in kg/m3 |
9.2 Betonstahl
9.2.1 Allgemeines
(1) Dieser Abschnitt gilt für Betonstabstahl und Betonstahlmatten im Lieferzustand nach den Normen der Reihe DIN 488 und nach allgemeinen bauaufsichtlichen Zulassungen. Für Betonstahl, der in Ringen produziert wurde, gelten die Anforderungen für den Zustand nach dem Richten.
(2) Betonstähle nach allgemeiner bauaufsichtlicher Zulassung dürfen für Betone ab der Fertigkeitsklasse C70/85 nur verwendet werden, sofern dies in der Zulassung geregelt ist.
9.2.2 Eigenschaften
(1) Die Festlegungen und konstruktiven Regeln in dieser Norm beziehen sich auf schweißgeeignete, gerippte Betonstähle mit einer charakteristischen Streckgrenze vonfyk = 500N/mm2 und den sonstigen in Tabelle 11 angegebenen Eigenschaften gleichermaßen für Zug- und Druckbeanspruchung. Für Stähle mit Eigenschaften, die von den in Tabelle 11 angegebenen abweichen, können andere als die in dieser Norm angegebenen Festlegungen und konstruktiven Regeln notwendig sein.
(2) Für Betonstähle nach allgemeinen bauaufsichtlichen Zulassungen sind die Duktilitätsmerkmale (normalduktil oder hochduktil) darin geregelt. Falls dort keine entsprechenden Festlegungen getroffen sind, sind die Betonstähle als normalduktil einzustufen.
(3) Die Streckgrenzefyk (Re nach den Normen der Reihe DIN 488) und die Zugfestigkeitftk (Rm nach den Normen der Reihe DIN 488) werden jeweils als charakteristische Werte definiert; sie ergeben sich aus der Last bei Erreichen der Streckgrenze bzw. der Höchstlast, geteilt durch den Nennquerschnitt.
(4) Für Erzeugnisse ohne ausgeprägte Streckgrenzefyk darf dafür der Wertf0,2k eingesetzt werden (siehe Bild 26).
(5) Betonstähle aller Lieferformen weisen die für die Bemessung erforderlichen Eigenschaften im Temperaturbereich zwischen -60°C und 200°C auf. Bei einer einmaligen Über- oder Unterschreitung dieses Temperaturbereiches ist mit deutlich veränderten Baustoffeigenschaften zu rechnen (siehe auch 12.3.2 (3)).
(6) Die Eignung zum Biegen ist durch das Verhalten der Betonstähle beim Rückbiegeversuch gekennzeichnet. Die in Tabelle 11 angegebenen Werte gelten für Temperaturen über -10°C.
(7) Betonstähle müssen eine Schweißeignung aufweisen, die für die vorgesehene Verbindung und die in Tabelle 12 genannten Schweißverfahren ausreicht. Für die Ausführung der Schweißarbeiten gilt DIN 4099-1.
Tabelle 11 - Eigenschaften der Betonstähle
| Zeile | Spalte | 1 | 2 | 3 | 4 | 5 | |
| Benennunga | BSt 500 S(A) |
BSt 500 M(A) |
BSt 500 S(B) |
BSt 500 M(B) |
Art der Anforderung bzw. Quantilwertp in % | ||
| 1 | Erzeugnisform | Betonstahl | Betonstahlmatten | Betonstahl | Betonstahlmatten | ||
| 2 | Duktilität | normal | hoch | ||||
| 3 | Streckgrenze fyk in N/mm2 | 500 | 5 | ||||
| 4 | Verhältnis (ft/fy)k | > 1,05 | > 1,08 | min. 10 | |||
| 5 | Verhältnis (fy/fyk)0,90
(fy = tatsächliche Streckgrenze) |
- | < 1,3 | max. 10 | |||
| 6 | Stahldehnung unter Höchstlastεukino/oo | 25 | 50 | 10 | |||
| 7 | Kennwert für die ErmüdungsfestigkeitN = 2 * 106 b in N/mm2 (mit einer oberen Spannung von nicht mehr als 0,6fy)b | ds< 28 | 190 | 100 | 190 | 100 | 10 |
| ds > 28 | - | - | 150 | - | |||
| 8 | Bezogene RippenflächefR für Nenndurchmesserds (in mm) | min. 5 | |||||
| 5,0 bis 6,0
6,5 bis 8,5 9,0 bis 10,5 11,0 bis 40,0 |
0,039
0,045 0,052 0,056 |
||||||
| 9 | Unterschreitung des Nennquerschnitts in % | 4 | max. 5 | ||||
| 10 | Biegerollendurchmesser beim Rückbiegeversuch für Nenndurchmesserds (in mm) | min. 1 | |||||
| 6 bis 12
14 bis 16 20 bis 25 28 bis 40 |
5ds
6ds 8ds 10ds |
||||||
| a | S: Betonstahl; M: Betonstahlmatten; A: normale Duktilität; B: hohe Duktilität |
| b | Falls höhere Werte im Versuch nachgewiesen werden, dürfen die Bemessungswerte nach Tabelle 16 entsprechend abgeleitet werden. |
Tabelle 12 - Zulässige Schweißverfahren und Anwendungsfälle
| Zeile | Spalte | 1 | 2 | 3 | |
| Belastungsart | Schweißverfahren mit Kurzbezeichnung und Ordnungsnummer des Schweißprozesses nach DIN EN ISO 4063 | Zugstäbea | Druckstäbea | ||
| 1 | Vorwiegend ruhend | Abrennstumpfschweißen (RA) | 24 | Stumpfstoß | |
| 2 | Lichtbogenhandschweißen (E) und Metall-Lichtbogenschweißen (MF) | 111
114 |
Stumpfstoß mitds> 20 mm, Laschenstoß, Überlappstoß, Kreuzungsstoßc, Verbindung mit anderen Stahlteilen | ||
| 3 | Metall-Aktivgasschweißen (MAG)b | 135 | Laschenstoß, Überlappstoß, Kreuzungsstoßc, Verbindung mit anderen Stahlteilen | ||
| 4 | 136 | - | Stumpfstoß mitds> 20 mm | ||
| 5 | Reibschweißen (FR) | 42 | Stumpfstoß, Verbindung mit anderen Stahlteilen | ||
| 6 | Widerstandspunktschweißen (mit Einpunktschweißmaschine) | 21 | Überlappstoßd
Kreuzungsstoßb d |
||
| 7 | Nicht vorwiegend ruhend | Abbrennstumpfschweißen (RA) | 24 | Stumpfstoß | |
| 8 | Lichtbogenhandschweißen (E) | 111 | - | Stumpfstoß mitds> 16 mm | |
| 9 | Metall-Aktivgasschweißen (MAG) | 135
136 |
- | Stumpfstoß mitds> 20 mm | |
| a | Es dürfen gleiche Stabnenndurchmesser sowie benachbarte Stabdurchmesser verbunden werden. |
| b | Zulässiges Verhältnis der Stabnenndurchmesser sich kreuzender Stäbe> 0,57. |
| c | Für tragende Verbindungends< 16mm |
| d | Für tragende Verbindungends< 28 mm |
9.2.3 Spannungs-Dehnungs-Linie für die Schnittgrößenermittlung
(1) Bei nichtlinearen Verfahren der Schnittgrößenermittlung ist eine wirklichkeitsnahe Spannungs-Dehnungs-Linie nach Bild 26 mitεs<εuk anzusetzen.
(2) Vereinfachend darf auch ein bilinear idealisierter Verlauf der Spannungs-Dehnungs-Linie (siehe Bild 26) angenommen werden. Dabei darf fürfy der RechenwertfyR nach 8.5.1 angenommen werden.
9.2.4 Spannungs-Dehnungs-Linie für die Querschnittsbemessung
(1) Die Bemessung ist auf der Grundlage der Nennquerschnittsfläche und des Nenndurchmessers unter Ansatz der idealisierten Spannungs-Dehnungs-Linie nach Bild 27 durchzuführen.
(2) Vereinfachend darf auch ein horizontaler oberer Ast der Spannungs-Dehnungs-Linie nach Bild 27 angenommen werden.
(3) Für die Querschnittsbemessung istftk, cal mit 525 N/mm2 anzusetzen und die Stahldehnungεs auf den Wertεsu = 0,025 zu begrenzen.
Bild 26 - Spannungs-Dehnungs-Linie des Betonstahls für die Schnittgrößenermittlung
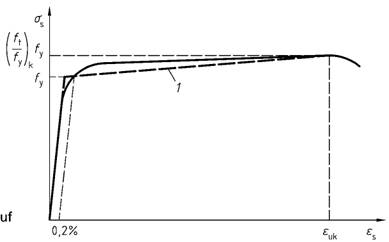
Legende
| 1 | idealisierter Verlauf |
Bild 27 - Rechnerische Spannungs-Dehnungs-Linie des Betonstahls für die Bemessung
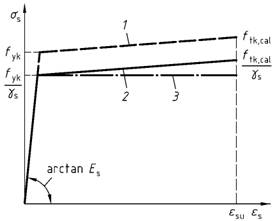
Legende
| 1 | idealisierter Verlauf |
| 2 | Verlauf für die Bemessung |
| 3 | vereinfachte Annahme für die Bemessung |
(4) Soweit in den Normen der Reihe DIN 488 oder in den allgemeinen bauaufsichtlichen Zulassungen nicht abweichend festgelegt, dürfen für die Bemessung folgende physikalische Eigenschaften des Betonstahls angenommen werden:
9.3 Spannstahl
9.3.1 Allgemeines
(1) Dieser Abschnitt gilt für Drähte, Litzen und Stäbe, die als Spannstahl in Betontragwerken verwendet werden.
(2) Die Anforderungen gelten für das Erzeugnis im Lieferzustand.
(3) Für die Produktgruppen, das Herstellungsverfahren, die Eigenschaften, die Prüfverfahren und das Verfahren zum Übereinstimmungsnachweis gelten die Festlegungen der allgemeinen bauaufsichtlichen Zulassungen.
9.3.2 Eigenschaften
(1) Das Verhalten des Spannstahls ist durch folgende Eigenschaften bestimmt:
Die 0,1 %-Dehngrenzefp0,1k und die Zugfestigkeitfpk werden jeweils als charakteristische Werte definiert.
(2) Die Spannstähle müssen die in dieser Norm vorausgesetzten Eigenschaften erfüllen.
(3) Die Toleranzen und Angaben zur Oberflächengestalt der Spannstähle sind den allgemeinen bauaufsichtlichen Zulassungen zu entnehmen.
Bild 28 - Spannungs-Dehnungs-Linie des Spannstahls für die Schnittgrößenermittlung

Legende
| 1 | idealisierter Verlauf |
(4) Bei nichtlinearen Verfahren der Schnittgrößenermittlung ist eine wirklichkeitsnahe Spannungs-Dehnungs-Linie nach Bild 28 anzunehmen.
(5) Vereinfachend darf der Verlauf der Spannungs-Dehnungs-Linie bilinear idealisiert angesetzt werden (siehe Bild 28). Hierbei dürfen fürfp0,1 undfp die Rechenwertefp0,1R bzw.fpR nach 8.5.1 angenommen werden.
(6) Es darf im Allgemeinen angenommen werden, dass Spannglieder im nachträglichem Verbund und Spannglieder ohne Verbund eine hohe Duktilität und Spannglieder im sofortigem Verbund eine normale Duktilität aufweisen.
9.3.3 Spannungs-Dehnungs-Linie für die Querschnittsbemessung
(1) Die Bemessung ist auf der Grundlage der Nennquerschnittsfläche des Spannstahls unter Ansatz der rechnerischen Spannungs-Dehnungs-Linie in Bild 29 durchzuführen.
(2) Vereinfachend darf ein horizontaler oberer Ast der Spannungs-Dehnungs-Linie nach Bild 29 angenommen werden.
(3) Für die Querschnittsbemessung ist die Stahldehnungεp auf den Wert (εp(0) + 0,025) zu begrenzen. Dabei istεp(0) die Vordehnung des Spannstahls.
(4) Die Spannungs-Dehnungs-Linie in Bild 29 ist für Temperaturen von -20°C bis +200°C gültig.
(5) Soweit in den allgemeinen bauaufsichtlichen Zulassungen nicht abweichend festgelegt, dürfen für die Bemessung folgende physikalische Eigenschaften des Spannstahls angenommen werden:
| - Wärmedehnzahl:α | = 10 * 10-6 K-1 |
| - Elastizitätsmodul:Ep | = 195000 N/mm2 (Litzen) = 205 000 N/mm2 (Stäbe und Drähte) |
Im Temperaturbereich zwischen -20'C und +200'C dürfen die vorgenannten Werte als charakteristische Werte verwendet werden.
Bild 29 - Rechnerische Spannungs-Dehnungs-Linie des Spannstahls für die Querschnittsbemessung
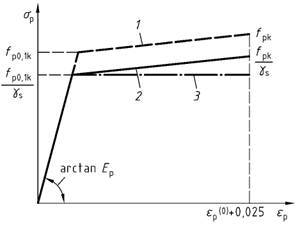
Legende
| 1 | idealisierter Verlauf |
| 2 | Verlauf für die Bemessung |
| 3 | vereinfachte Annahme für die Bemessung |
10 Nachweise in den Grenzzuständen der Tragfähigkeit
10.1 Allgemeines
In 10.2 bis 10.4 werden Festlegungen für die ungestörten Bereiche von Balken, Platten und ähnlichen Bauteilen getroffen, in denen ein Ebenbleiben der Querschnitte angenommen werden darf. Die Störbereiche dieser Bauteile sowie wandartige Träger und andere Bauteile mit nicht eben bleibenden Querschnitten dürfen nach 10.6 bemessen und konstruktiv durchgebildet werden.
10.2 Biegung mit oder ohne Längskraft und Längskraft allein
(1) Bei der Bestimmung der Grenztragfähigkeit von bewehrten Querschnitten gelten folgende Annahmen:
(2) Bei unbewehrten Querschnitten gelten die folgende Annahmen und Grundsätze:
(3) Die Dehnungen des Betons sind aufεc2u oderεlc2u nach Tabelle 9 bzw. Tabelle 10 und die Dehnungen des Betonstahls und des Spannstahls aufεsu = + 0,025 bzw. (εp(0) + 0,025) zu begrenzen (siehe Bild 30).
(4) Bei vollständig überdrückten Querschnitten darf die Dehnung im Punkt C höchstensεc2 oderεlc2 nach Tabelle 9 bzw. Tabelle 10 betragen.
Bild 30 - Mögliche Dehnungsverteilungen im Grenzzustand der Tragfähigkeit (bei im Verbund liegenden Betonstahl und Spannstahl)
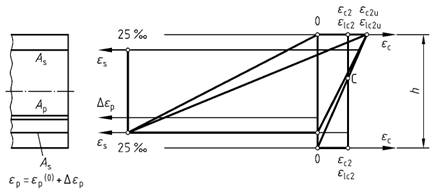
(5) Bei geringen Ausmitten bised/h< 0,1 darf für Normalbeton die günstige Wirkung des Kriechens des Betons vereinfachend durch die Wahl vonεc2 = - 0,0022 berücksichtigt werden.
(6) In vollständig überdrückten Platten von Plattenbalken, Kastenträgern oder ähnlichen gegliederten Querschnitten ist die Dehnung in der Plattenmitte aufεc2 oderεlc2 nach Tabelle 9 bzw. Tabelle 10 zu begrenzen. Die Tragfähigkeit des Gesamtquerschnitts braucht nicht kleiner angesetzt zu werden als diejenige der Stege mit der Höheh und der Dehnungsverteilung nach Bild 30.
(7) Bei Tragwerken mit exzentrisch geführten internen Spanngliedern ohne Verbund darf der Spannungszuwachs Δσp in diesen Spanngliedern vereinfacht mit 100N/mm2 angesetzt werden.
(8) Die Biegezugbewehrung ist unter Beachtung von 10.3.4 (9) zu ermitteln.
 |
weiter . |  |
(Stand: 01.03.2019)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: 90.- € netto (Grundlizenz)
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion
...
X
⍂
↑
↓