

umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (4)
 |
zurück |  |
8.5.2 Berechnungsansatz für stabförmige Bauteile und einachsig gespannte Platten bei Biegung mit oder ohne Längskraft
(1) Die Schnittgrößen stabförmiger Bauteile sowie einachsig gespannter Platten dürfen unter Ansatz von rechnerischen Momenten-Krümmungs-Beziehungen berechnet werden, denen das Ebenbleiben der Querschnitte zugrunde liegt.
(2) Auf dieser Grundlage können die Schnittgrößen für die Nachweise in den Grenzzuständen der Gebrauchstauglichkeit und der Tragfähigkeit ermittelt werden. Für den Nachweis in den Grenzzuständen der Tragfähigkeit gilt 8.5.1.
(3) Zur Vereinfachung darf die in Bild 10 angegebene trilineare Momenten-Krümmungs-Beziehung verwendet werden. Die Krümmungen (1/r)γ und (1/r)u sind dabei unter Berücksichtigung der Mitwirkung des Betons auf Zug zwischen den Rissen zu ermitteln.
Bild 10 -Vereinfachte Momenten-Krüm mungs-Beziehung
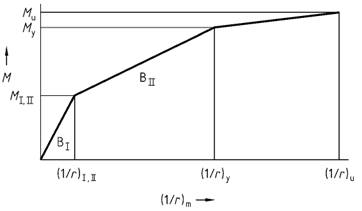
Legende
| BI,BII | Biegesteifigkeit im ungerissenen Zustand I bzw. . gerissenen Zustand II =dM/d(1/r) |
| MI, II | Moment beim Übergang von Zustand I zu Zustand II |
| My | Fließmoment |
| Mu | Bruchmoment |
| (1/r)I, II | zuMI, II gehörende Krümmung =MI, II/BI |
(4) Für Bauteile mit Längskrafteinwirkung gilt die vereinfachte Momenten-Krümmungs-Beziehung in Bild 10 in der dargestellten Weise nur dann, wenn die Bezugslinie für die Momentenermittlung mit der Wirkungslinie der Längskraft zusammenfällt. Unterscheiden sich diese, z.B. dann, wenn eine Vorspannung nicht in der Schwerachse wirkt, ist die Wirkung der daraus resultierenden Vorkrümmung zu berücksichtigen.
8.6 Stabförmige Bauteile und Wände unter Längsdruck (Theorie II. Ordnung)
8.6.1 Allgemeines
(1) Der Gleichgewichtszustand von Tragwerken mit stabförmigen Bauteilen oder Wänden unter Längsdruck und insbesondere der Gleichgewichtszustand dieser Bauteile selbst muss unter Berücksichtigung der Auswirkung von Bauteilverformungen nachgewiesen werden, wenn diese die Tragfähigkeit um mehr als 10 % verringern. Dies gilt für jede Richtung, in der ein Versagen nach Theorie II. Ordnung auftreten kann.
(2) Im Grenzzustand der Tragfähigkeit ist für die jeweils ungünstigste Einwirkungskombination nachzuweisen, dass in kritischen Querschnitten der Bemessungswert der Einwirkungen nach Theorie II. Ordnung den Bemessungswert des Tragwiderstands nicht überschreitet und das statische Gleichgewicht (örtlich und für das Gesamttragwerk) gesichert ist.
(3) Diese Grundsätze gelten auch für andere Tragwerke (z.B. Schalen) und Bauteile, bei denen Verformungen (gegebenenfalls örtliche, z.B. in Auflagerbereichen von wandartigen Trägern) die Tragfähigkeit wesentlich beeinflussen oder ein Verlust des stabilen Gleichgewichts zu befürchten ist (z.B. seitliches Ausweichen schlanker Träger, siehe 8.6.8).
(4) Die Bemessungswerte der einwirkenden Schnittgrößen sind unter Berücksichtigung von Maßungenauigkeiten und Unsicherheiten bezüglich Lage und Richtung von Längskräften zu ermitteln. Sofern keine anderen geeigneten Annahmen getroffen werden, sind diese Einflüsse durch Ansatz geometrischer Imperfektionen zu berücksichtigen (siehe 8.6.4).
(5) Nichtlineare Verfahren für das Gesamttragwerk nach 8.5 dürfen unter Berücksichtigung plastischer Gelenke nach 8.4 angewendet werden. Dabei sind aber plastische Gelenke (Krümmungen (1/r)m > (1/r)y nach Bild 10) für Bauteile unter Längsdruck im Sinne von Absatz (1) nicht zulässig.
(6) Werden die Schnittgrößen nach Theorie I. Ordnung mit einem Verfahren nach 8.2, 8.3 oder 8.4 ermittelt, sind die einwirkenden Schnittgrößen nach Theorie II. Ordnung oder die zusätzlich infolge Verformungen nach Theorie II. Ordnung zu berücksichtigenden Schnittgrößen mit dem Verfahren nach 8.5 zu ermitteln.
(7) Abweichend von Absatz (6) dürfen die Formänderungen auf der Grundlage von Bemessungswerten, die auf den Mittelwerten der Baustoffkennwerte beruhen (z.B.fcm/γc,Ecm/γc), ermittelt werden. Für die Ermittlung der Grenztragfähigkeit im kritischen Querschnitt sind dann jedoch die Bemessungswerte der Baustofffestigkeiten (z.B.α *fck/γc) anzusetzen.
(8) Die Mitwirkung des Betons auf Zug zwischen den Rissen darf auf der sicheren Seite liegend vernachlässigt werden.
8.6.2 Einteilung der Tragwerke und Bauteile
(1) Zur Nachweisführung werden Tragwerke oder Bauteile in ausgesteifte oder unausgesteifte eingeteilt, je nachdem, ob aussteifende Bauteile vorgesehen sind oder nicht, oder sie werden als verschieblich oder unverschieblich betrachtet, je nachdem, ob bei Tragwerken die Auswirkungen nach Theorie II. Ordnung entsprechend 8.6.1 (1) zu berücksichtigen sind bzw. bei Einzelbauteilen die gegenseitige Verschiebung der Stabenden von Bedeutung ist oder nicht.
(2) Ein aussteifendes Bauteil oder ein System aussteifender Bauteile muss eine ausreichende Steifigkeit haben, um alle horizontalen Lasten, die auf das Tragwerk wirken, aufzunehmen und in die Fundamente weiterzuleiten und um die Tragfähigkeit der auszusteifenden Tragwerksteile sicherzustellen.
(3) Zu Bauteilen im Sinne von Absatz (1) gehören Einzeldruckglieder mit der Ersatzlängel0. Sie können sein:
(4) Die Ersatzlängel0 =β *lcol von Einzeldruckgliedern (mit der Stützenlängelcol zwischen den idealisierten Einspannstellen) ist von den Steifigkeiten der Einspannungen an den Enden des Einzeldruckglieds und von der Verschieblichkeit der Enden des Druckglieds abhängig. Hinweise zur Berechnung der Ersatzlängel0 von Einzeldruckgliedern können dem DAfStb-Heft 525 entnommen werden. Die Schlankheit der Einzeldruckglieder errechnet sich ausλ =l0/i, wobei i der Trägheitsradius des Querschnitts ist.
(5) Sofern keine genaueren Nachweise geführt werden, dürfen Tragwerke, die durch lotrechte Bauteile wie z.B. massive Wandscheiben oder Bauwerkskerne ausgesteift sind, als unverschieblich im Sinne von Absatz (1) angesehen werden, wenn folgende Bedingungen erfüllt sind:
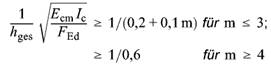 |
(25) |
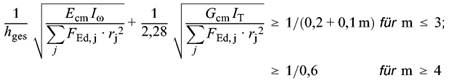 |
(26) |
Bild 11 - Arten von Einzeldruckgliedern
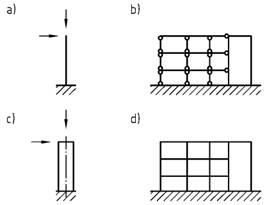
Legende
Dabei ist
| m | die Anzahl der Geschosse |
| hges | die Gesamthöhe des Tragwerkes von der Fundamentoberkante oder einer nicht verformbaren Bezugsebene |
| rj | der Abstand der Stütze j vom Schubmittelpunkt des Gesamtsystems |
| FEd | die Summe der Bemessungswerte der Vertikallasten mitγF = 1,0 |
| FEd, j | der Bemessungswert der Vertikallast der Stützej mitγF = 1,0 |
| EcmIc | die Summe der Nennbiegesteifigkeiten aller vertikalen aussteifenden Bauteile, die in der betrachteten Richtung wirken und den Anforderungen nach 8.6.2 (2) genügen. In den aussteifenden Bauteilen sollte die Betonzugspannung unter der maßgebenden Einwirkungskombination nicht den Wertfctm nach Tabelle 9 oder Tabelle 10 überschreiten. Wenn die Steifigkeit der aussteifenden Bauteile über ihre Höhe veränderlich ist, sollte eine Ersatzsteifigkeit eingeführt werden |
| EcmIϖ | die Summe der Nennwölbsteifigkeiten aller gegen Verdrehung aussteifenden Bauteile |
| GcmIT | die Summe der Torsionssteifigkeiten aller gegen Verdrehung aussteifenden Bauteile (St. Vernant'sche Torsionssteifigkeit) |
8.6.3 Nachweisverfahren
(1) Bei Einzeldruckgliedern darf durch Vergleich der Schlankheit mit Grenzwerten entschieden werden, ob Auswirkungen nach Theorie II. Ordnung zu berücksichtigen sind.
(2) Unverschiebliche und verschiebliche Einzeldruckglieder gelten als schlank, wenn folgende Grenzwerte der Schlankheit überschritten werden:
| λmax = 25 | für |νEd|> 0,41 | (27) |
| λmax = 16 | für |νEd| < 0,41 | (28) |
| mit | ||
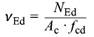 |
(29) |
Dabei ist
| NEd | der Bemessungswert der mittleren Längskraft des Einzeldruckglieds |
| Ac | die Querschnittsfläche des Druckglieds |
| fcd | der Bemessungswert der Betondruckfestigkeit nach 9.1.6 (2) |
(3) Unverschiebliche Tragwerke oder Einzeldruckglieder, die als nicht schlank gelten, brauchen nicht nach Theorie II. Ordnung bemessen zu werden.
(4) Einzeldruckglieder in unverschieblich ausgesteiften Tragwerken brauchen, selbst wenn sie als schlank gelten, nicht nach Theorie II. Ordnung untersucht zu werden, wenn ihre Schlankheitλ kleiner oder gleich dem Wert nach Gleichung (30) ist. Dies gilt nur dann, wenn die Stütze zwischen ihren Enden nicht durch Querlasten oder Lastmomente beansprucht wird und die Längskraft über die Stützenlänge als konstant angenommen werden kann.
| λcrit = 25 (2 -e01/e02) | (30) |
Dabei ist
| e01/e02 | das Verhältnis der jeweiligen Lastausmitten der Längskraft an den Stützenenden (siehe Bild 13) mit |e01|< |e02| |
Für den Sonderfall der beidseitig gelenkig gelagerten Stütze giltλcrit = 25.
Für die Bemessung der Stabenden gilt Absatz (9).
(5) Kriechauswirkungen dürfen in der Regel vernachlässigt werden, wenn die Stützen an beiden Enden monolithisch mit lastabtragenden Bauteilen verbunden sind oder wenn bei verschieblichen Tragwerken die Schlankheit des Druckgliedesλ < 50 und gleichzeitig die bezogene Lastausmittee0/h > 2 ist.
(6) Für schlanke Einzeldruckglieder dürfen die Auswirkungen nach Theorie II. Ordnung vereinfachend nach dem Modellstützenverfahren nach 8.6.5 ermittelt werden.
(7) Für Nachweise am Gesamttragwerk nach Theorie I. Ordnung wird auf DAfStb-Heft 525 verwiesen.
(8) Wird bei verschieblichen Tragwerken eine Einspannung der Stabenden des Druckgliedes durch anschließende Bauteile angenommen (z.B. durch einen Rahmenriegel), sind diese anschließenden einspannenden Bauteile auch für diese Zusatzbeanspruchung zu bemessen.
(9) Einzeldruckglieder sollten bei Anwendung der Regelung nach Absatz (4) an beiden Enden mindestens so bemessen werden, dass die folgende Bedingungen eingehalten werden:
| MRd> |NEd| *h/20 | (31) |
| NRd> |NEd| | (32) |
Dabei ist
| h | die Abmessung des Querschnitts der Stütze in der betrachteten Richtung |
8.6.4 Imperfektionen
(1) Für Einzeldruckglieder dürfen die geometrischen Ersatzimperfektionen durch eine Erhöhung der Lastausmitte der Längskräfte um eine zusätzliche ungewollte Lastausmitteea, die in ungünstigster Richtung wirkt, erfasst werden:
| ea =αa1 *l0/2 | (33) |
Dabei ist
| l0 | die Ersatzlänge des Einzeldruckgliedes nach 8.6.2 (4) |
| αa1 | die Schiefstellung gegen die Sollachse nach Gleichung (4) mithges =lcol |
Ist das Einzeldruckglied aussteifendes Bauteil in einem Tragwerk nach Bild 11 b), ist zu untersuchen, ob sich bei Ansatz der Schiefstellungαa1 des gesamten Tragwerks (aussteifende und auszusteifende Bauteile) gegen die Sollachse nach 7.2 eine größere Ausmitteea des aussteifenden Einzeldruckgliedes als nach Gleichung (33) ergibt. Der ungünstigere Wert ist anzusetzen.
(2) Imperfektionen nach Absatz (1) brauchen nur bei Nachweisen nach Theorie II. Ordnung angesetzt zu werden.
8.6.5 Modellstützenverfahren
(1) Das im Folgenden beschriebene Modellstützenverfahren gilt für Druckglieder mit rechteckigem oder rundem Querschnitt, bei denen die Lastausmitte nach Theorie I. Ordnung die Bedingunge0> 0,1h (mit der Dicke des Querschnittsh in der betrachteten Ebene) erfüllt.
(2) Für andere Querschnittsformen und für Lastausmittene0 < 0,1h ist das Modellstützenverfahren auch anwendbar, jedoch sind andere Näherungen geeigneter. 7)
(3) Eine Modellstütze ist eine Kragstütze mit der Längel =l0/2, die
Bild 12 - Modellstütze
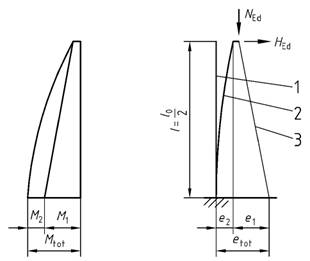
Legende
| 1 | planmäßig gerade Stabachse |
| 2 | Biegelinie nach Theorie II. Ordnung |
| 3 | Wirkungslinie der Resultierenden vonNEd undHEd |
(4) Der Nachweis des Gleichgewichts wird durch die Bemessung im kritischen Querschnitt am Fuß der Modellstütze (siehe Bild 12) auf der Grundlage der Krümmung (1/r) des Querschnitts unter der maximalen Auslenkung der Stütze nach Theorie II. Ordnung erbracht.
(5) Die Gesamtausmitte für die Modellstütze ergibt sich bei Einzeldruckgliedern mit konstantem Querschnitt (bezüglich Beton und Bewehrungsquerschnitt, wobei Stoßbereiche vernachlässigt werden) im am stärksten beanspruchten (kritischen) Querschnitt zu:
| etot =e1 +e2 | (34) |
| mit | |
| e1 =e0 +ea | (35) |
Dabei ist
| e0 | die planmäßige Lastausmitte nach Theorie I. Ordnung =MEd0/NEd |
| MEd0 | der Bemessungswert des aufzunehmenden Biegemoments nach Theorie 1. Ordnung |
| NEd | der Bemessungswert der aufzunehmenden Längskraft |
| ea | die zusätzliche ungewollte Lastausmitte nach Gleichung (33) |
| e2 | die zusätzliche Lastausmitte infolge Auswirkungen nach Theorie II. Ordnung |
(6) Für Druckglieder in unverschieblichen Rahmentragwerken, die einen konstanten Querschnitt aufweisen und durch Momente beansprucht werden, deren Verlauf über die Stützenlänge linear veränderlich ist, mit gleichen (siehe Bild 13 a)) oder mit unterschiedlichen Werten der Lastausmitten an beiden Enden (siehe Bild 13 b) und c)), darf vereinfachend die wirksame Lastausmittee0 im kritischen Querschnitt nach den Gleichungen (36) oder (37) angesetzt werden; der größere Wert ist maßgebend.
| e0 = 0,6e02 + 0,4e01 | (36) |
| e0 = 0,4e02 | (37) |
Dabei ist
| e01,e02 | die jeweilige planmäßige Ausmitte der Längskraft nach Theorie I. Ordnung an den beiden Stützenenden mit |e02|> |e01| |
Bild 13 - Bemessungsmodell zur Berechnung der wirksamen Lastausmitte
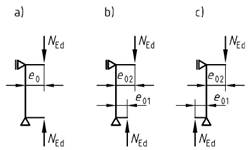
Legende
(7) Die zusätzliche Lastausmittee2 infolge Auswirkungen nach Theorie II. Ordnung ist auf der Grundlage von 8.6.1 zu ermitteln.
(8) Vereinfachend darf die maximale Auslenkung, die der zusätzlichen Lastausmittee2 nach Theorie II. Ordnung entspricht, wie folgt angenommen werden:
| e2 =K1 * (1/r) *l02/10 | (38) |
Dabei ist
| l0 | die Ersatzlänge der Stütze nach 8.6.2 (4) | |
| (1/r) | die Krümmung im kritischen Querschnitt | |
| K1 | =λ /10 - 2,5 | für 25<λ< 35 |
| = 1 | fürλ > 35 |
(9) Näherungsweise darf die Krümmung 1/r im kritischen Querschnitt ermittelt werden aus:
| (1/r) = 2K2 *εyd / (0,9d) | (39) |
mit
| K2 = (Nud -NEd) / (Nud -Nbal)< 1 | (40) |
Dabei ist
| εyd | der Bemessungswert der Dehnung der Bewehrung an der Streckgrenze =fyd/Es |
| d | die Nutzhöhe des Querschnitts in der zu erwartenden Richtung des Stabilitätsversagens |
| NEd | der Bemessungswert der aufzunehmenden Längskraft (für Druck negativ) |
| Nud | der Bemessungswert der Grenztragfähigkeit des Querschnitts, der nur durch zentrischen Druck beansprucht wird. Er darf angenommen werden zuNud = - (fcd *Ac +fyd *As) |
| Nbal | die aufnehmbare Längsdruckkraft bei größter Momententragfähigkeit des Querschnitts. Bei symmetrisch bewehrten rechteckigen Querschnitten darf sie näherungsweise zuNbal = - (0,4fcd *Ac) angenommen werden. |
Die AnnahmeK2 = 1 liegt stets auf der sicheren Seite.
8.6.6 Druckglieder mit zweiachsiger Lastausmitte
(1) Ist es erforderlich, das Tragverhalten in jeder der beiden Hauptachsenrichtungen zu betrachten, muss der kritische Querschnitt für beide Fälle nachgewiesen werden. Für beide Richtungen können an den Enden des Bauteils unterschiedliche Randbedingungen vorliegen. Diese Bedingungen müssen in einer geeigneten Weise erfasst werden.
(2) Für Druckglieder mit rechteckigem Querschnitt dürfen getrennte Nachweise in den Richtungen der beiden Hauptachsenγ undz (siehe Bild 14) geführt werden, wenn das Verhältnis der bezogenen Lastausmittene0y/b unde0z/h eine der folgenden Bedingungen erfüllt:
| (e0z/h) / (e0y/b)< 0,2 | (41) |
| oder | |
| (e0y/b) / (e0z/h)< 0,2 | (42) |
Dabei ist
| e0y,e0Z | die jeweilige Lastausmitte nach Theorie I. Ordnung in Richtung der Querschnittsseitenb bzw.h |
Dies bedeutet, dass der Lastangriffspunkt vonNEd innerhalb der schraffierten Bereiche in Bild 14 liegt. Ein genauerer Nachweis wird erforderlich, wenn die beiden Bedingungen nach Gleichung (41) und Gleichung (42) nicht erfüllt sind.
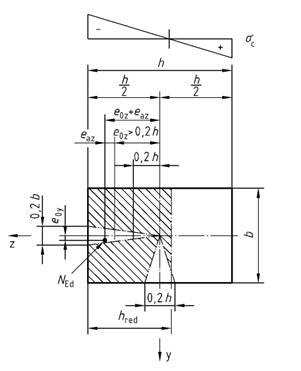
(3) Für Druckglieder mit rechteckigem Querschnitt und mite0Z > 0,2h dürfen getrennte Nachweise nur dann geführt werden, wenn der Nachweis der Biegung über die schwächere Hauptachsez des Querschnitts auf der Grundlage der reduzierten Querschnittsdickehred nach Bild 15 geführt wird. Der Werthred darf unter der Annahme einer linearen Spannungsverteilung nach folgender Gleichung ermittelt werden:
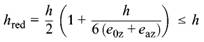 |
(43) |
Dabei ist
| h | die größere der beiden Querschnittsseiten |
| eaz | die Zusatzausmitte zur Berücksichtigung geometrischer Ersatzimperfektionen inz-Richtung nach Gleichung (33) |
| e0z | die Lastausmitte nach Theorie I. Ordnung in Richtung der Querschnittsseiteh |
Bild 14 - Grenzen für getrennte Nachweise in Richtung der beiden Hauptachsen
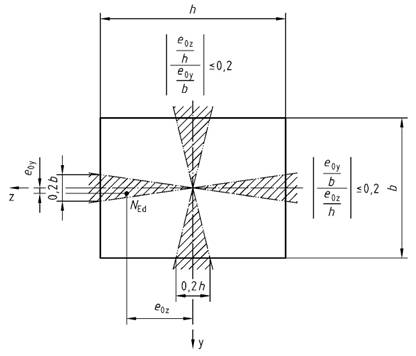
Bild 15 - Reduzierte Querschnittsdickehred für den getrennten Nachweis inγ-Richtung beie0z > 0,2h
8.6.7 Druckglieder aus unbewehrtem Beton
(1) Unabhängig vom Schlankheitsgradλ sind Druckglieder aus unbewehrtem Beton als schlanke Bauteile zu betrachten. Jedoch ist für Druckglieder aus unbewehrtem Beton mitlcol/h < 2,5 eine Schnittgrößenermittlung nach Theorie II. Ordnung nicht erforderlich.
(2) Die Schlankheit am Einbauort betonierter unbewehrter Wände oder Stützen sollte im Allgemeinen den Wertλ = 85 nicht überschreiten.
(3) Die von einer schlanken Stütze oder Wand aus unbewehrtem Beton in unverschieblich ausgesteiften Tragwerken aufnehmbare Längsdruckkraft darf näherungsweise wie folgt berechnet werden:
| NRd = - (b *h *fcd *Φ) | (44) |
mit
| Φ = 1,14 (1 - 2etot/h) - 0,02l0/h und 0<Φ< 1 - 2etot/h | (45) |
Dabei ist
| NRd | der Bemessungswert der aufnehmbaren Längsdruckkraft |
| b | die Breite des Querschnitts |
| h | die Dicke des Querschnitts |
| Φ | der Beiwert zur Berücksichtigung der Auswirkungen nach Theorie II. Ordnung auf die Tragfähigkeit von Druckgliedern aus unbewehrtem Beton in unverschieblich ausgesteiften Tragwerken |
| etot | die Gesamtausmitte =e0 +ea +eΦ |
| e0 | die Lastausmitte nach Theorie I. Ordnung, nach Erfordernis unter Berücksichtigung der Einwirkungen aus anschließenden Decken (z.B. Biegemomente infolge einer Einspannung, die von einer Platte auf die Wand übertragen werden) sowie aus horizontalen Windeinwirkungen |
| ea | die ungewollte zusätzliche Lastausmitte infolge geometrischer Imperfektionen. Fehlen genauere Angaben, darf,ea = 0,5l0/200 angenommen werden |
| eΦ | die Ausmitte infolge Kriechen; im Allgemeinen kann der Anteilea vernachlässigt werden Weitere Angaben können DAfStb-Heft 525 entnommen werden. |
Weitere Angaben können DAfStb-Heft 525 entnommen werden.
8.6.8 Seitliches Ausweichen schlanker Träger
(1) Die Sicherheit schlanker Träger gegen seitliches Ausweichen ist nachzuweisen.
(2) Sie darf als ausreichend angenommen werden, wenn die Anforderung nach Gleichung (46) erfüllt ist. Anderenfalls sollte ein genauerer Nachweis geführt werden.
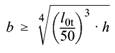 |
(46) |
Dabei ist
| b | die Breite des Druckgurts |
| h | die Höhe des Trägers |
| l0t | die Länge des Druckgurts zwischen seitlichen Abstützungen |
(3) Schlanke Fertigteilträger müssen während des Anhebens, des Transports und der Montage gegen seitliches Ausweichen ausreichend gesichert sein.
(4) Die Nachweisführung schlanker Träger im Endzustand einschließlich ihrer Auflager muss eine unbeabsichtigte ausmittige Auflagerung berücksichtigen.
(5) Sofern keine genaueren Angaben vorliegen, ist die Auflagerkonstruktion so zu bemessen, dass sie mindestens ein TorsionsmomentTEd aus dem Träger nach Gleichung (47) aufnehmen kann.
| TEd =VEd *leff/300 | (47) |
Dabei ist
| leff | die effektive Stützweite des Trägers |
| VEd | der Bemessungswert der Auflagerkraft rechtwinklig zur Trägerachse |
(6) Bei genaueren Nachweisen der Kippsicherheit sollten die Schnittgrößen am verformten Trräger nach 8.6.1 (7) ermittelt werden.
Imperfektionen sind dabei in geeigneter Weise, z.B. durch den Ansatz geometerischer Ersatzimperfektionen, zu berücksichtigen. Sofern keine genauen Angaben vorliegen, darfea =leff /300 angesetzt werden.
8.7 Vorgespannte Tragwerke
8.7.1 Allgemeines
(1) Vorspannung mittels Spanngliedern kann als eine Einwirkung aus Anker- und Umlenkkräften oder als einwirkende Schnittgröße betrachtet werden.
(2) Alternativ dazu ist auch eine Berücksichtigung der Vorspannung als Dehnungszustand mit entsprechender Vorkrümmung möglich. Dann wird die Vordehnung beim Widerstand des Bauteilquerschnitts berücksichtigt.
(3) Die Verfahren nach Absatz (1) und Absatz (2) führen zum gleichen Bemessungsergebnis (siehe Bild 16), wenn jeweils Spannungen und Dehnungen im Spannbettzustand als Vorspannung bzw. Vordehnung bezeichnet werden und im Grenzzustand der Tragfähigkeit der Spannstahl nicht plastiziert. Als Spannbettzustand wird der Spannungs- und Dehnungszustand im Spannstahl zu einem beliebigen Zeitpunktt bezeichnet, der dem spannungsfreien Betonquerschnitt unter Berücksichtigung zeitabhängiger Verformungen des Spannstahls und des Betons entspricht.
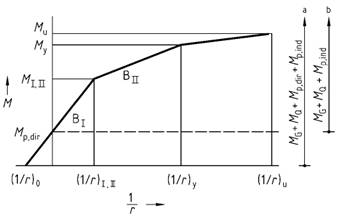
Bild 16 - Vereinfachte Momenten-Krümmungs-Beziehung für Spannbetonquerschnitte
Legende
| BI,BII | Biegesteifigkeit im ungerissenen (Zustand I) bzw. . gerissenen Zustand (Zustand II) =dM /d(1/r) |
| (1/r)0 | Vorkrümmung infolge Vorspannung |
| Mp, dir | statisch bestimmte Anteil des Moments aus Vorspannung |
| Mp, ind | statisch unbestimmte Anteil des Moments aus Vorspannung |
| MI, II | Moment beim Übergang von Zustand I zu Zustand II |
| My | Fließmoment |
| Mu | Bruchmoment |
| (1/r)I, II | |
| a Einwirkende Momente bei Anwendung von Absatz (1) | |
| b Einwirkende Momente bei Anwendung von Absatz (2) | |
(4) Für die Schnittgrößenermittlung von vorgespannten Tragwerken dürfen alle in 8.1 aufgeführten Verfahren angewendet werden.
(5) Bei Anwendung linear-elastischer Verfahren der Schnittgrößenermittlung sollte die statisch unbestimmte Auswirkung der Vorspannung als Einwirkung berücksichtigt werden. Bei Anwendung nichtlinearer Verfahren sowie bei der Ermittlung der erforderlichen Rotation bei Verfahren nach der Plastizitätstheorie sollte die Vorspannung als Vordehnung mit entsprechender Vorkrümmung berücksichtigt werden. Die Ermittlung des statisch unbestimmten Moments aus Vorspannung entfällt dann, da bei diesen Verfahren die Schnittgrößen infolge Vorspannung nicht getrennt von den Lastschnittgrößen ausgewiesen werden können.
(6) Wird ein Verfahren nach der Plastizitätstheorie für die Schnittgrößenermittlung von vorgespannten stabförmigen Bauteilen im Grenzzustand der Tragfähigkeit verwendet, ist stets das Rotationsvermögen nach 8.4.2 nachzuweisen.
(7) Bei Spanngliedern ohne Verbund sollte die Schnittgrößenermittlung im Allgemeinen nach Absatz (1) durchgeführt werden. Dabei sollte bei im Betonquerschnitt geführten Spanngliedern der Anstieg der Spanngliedkraft über den Spannbettzustand hinaus infolge der Verformung des Tragwerks berücksichtigt werden.
(8) Bei Spanngliedern mit Verbund sollte bei der Schnittgrößenermittlung der Spannstahl als in starrem Verbund mit dem Beton liegend angenommen werden. Der Anstieg der Spanngliedkraft infolge Tragwerksverformung vor Herstellung des Verbundes darf vernachlässigt werden (z.B. bei Bauteilen im Bauzustand).
(9) Externe Spannglieder dürfen auf der freien Länge zwischen Umlenkelementen als gerade angenommen werden.
(10) Bei extern angeordneten Spanngliedern ist die Dehnung zwischen zwei aufeinander folgenden Kontaktpunkten mit dem Tragwerk konstant. Die Dehnung ist unter Berücksichtigung der Verformung des Tragwerks zu bestimmen.
(11) Wenn bei Tragwerken mit externen Spanngliedern die Schnittgrößenermittlung für das gesamte Tragwerk vereinfachend linear-elastisch erfolgt, darf der Spannungszuwachs im Spannstahl infolge Tragwerksverformungen unberücksichtigt bleiben.
 |
weiter . |  |
(Stand: 01.03.2019)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: ab 105.- € netto
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion