

 |
zurück |  |
| Bestimmung der Ökotoxizität
C.13 Biokonzentration: Durchfluß-Fischtest |
Anhang V zur RL 67/548/EWG |
Anhang 1 zur RL 67/548/EWG Anhang V C.13.
Chemische Eigenschaften eines geeigneten Verdünnungswassers
| >Substanz | Grenzkonzentration |
| 1 Partikelstoffe | 5 mg/l |
| 2 Gesamter organischer Kohlenstoff | 2 mg/l |
| 3 Nichtionisiertes Ammoniak | 1 µg/I |
| 4 Restchlor | 10 µg/I |
| 5 Gesamte phosphororganische Pestizide | 50 ng/l |
| 6 Gesamte chlororganische Pestizide sowie polychlorierte Biphenyle | 50 ng/l |
| 7 Gesamter organischer Chlorgehalt | 25 ng/l |
| 8 Aluminium | 1 µg/I |
| 9 Arsen | 1 µg/I |
| 10 Chrom | 1 µg/I |
| 11 Kobalt | 1 µg/I |
| 12 Kupfer | 1 µg/I |
| 13 Eisen | 1 µg/I |
| 14 Blei | 1 µg/I |
| 15 Nickel | 1 µg/I |
| 16 Zink | 1 µg/I |
| 17 Cadmium | 100 ng/l |
| 18 Quecksilber | 100 ng/l |
| 19 Silber | 100 ng/l |
Anhang 2 zur RL 67/548/EWG Anhang V C.13.
Für den Test empfohlene Fischspezies
| Empfohlene Spezies | Bereich der Testtemperatur |
Gesamtlänge der Versuchstiere |
|
| (°C) | (cm) | ||
| 1 | Danio rerio1 (Teleostei, Cyprinidae) (Hamilton-Buchanan) Zebrabärbling | 20-25 | 3,0 ± 0,5 |
| 2 | Pimephales promelas (Teleostei, Cyprinidae) (Rafinesque) Dickkopf-Elritye | 20-25 | 5,0 ± 2,0 |
| 3 | Cyprinus carpio (Teleostei, Cyprinidae) (Linnaeus) Karpfen | 20-25 | 5,0 ± 3,0 |
| 4 | Oryzias latipes (Teleostei, Poeciliidae) (Temminck und Schlegel) Japanischer Reisfisch | 20-25 | 4,0 ± 1,0 |
| 5 | Poecilia reticulata (Teleostei, Poeciliidae) (Peters) Guppy | 20-25 | 3,0 ± 1,0 |
| 6 | Lepomis macrochirus (Teleostei, Centrarchidae) (Rafi- nesque) Blauer Sonnenbarsch | 20-25 | 5,0 ± 2,0 |
| 7 | Oncorhynchus mykiss (Teleostei, Salmonidae) (Walbaum) Regenbogenforelle | 13-17 | 8,0 ± 4,0 |
| 8 | Gasterosteus aculeatus (Teleostei, Gasterosteidae) (Linnaeus) Dreistachliger Stichling | 18-20 | 3,0 ± 1,0 |
| 1) Meyer A., Orti G. (1993) Proc. Royal Society of London, Series B., Vol. 252, p. 231. | |||
In verschiedenen Ländern wurden unterschiedliche Ästuarine- und Meeresspezies verwendet, beispielsweise:
| Umberfisch | Leiostomus xanthurus |
| Edelsteinkärpfling | Cyprinodon variegatus |
| Gezeiten-Ährenfisch | Menidia beryllina |
| Juwelflußbarsch | Cymatogaster aggregata |
| Englische Seezunge | Parophrys vetulus |
| Geweihgroppe | Leptocottus armatus |
| Dreistachliger Stichling | Gasterosteus aculeatus |
| Sägebarsch | Dicentracus labrax |
| Ukelei | Alburnus alburnus |
Zusammenstellung
Die in obenstehender Tabelle aufgeführten Süßwasserfische sind leicht zu züchten oder stehen größtenteils ganzjährig zur Verfügung, wohingegen die Verfügbarkeit der Ästuarinen- und Meeresspezies teilweise auf bestimmte Länder beschränkt ist. Sie können entweder in Teichwirtschaften oder im Labor unter krankheits- und parasitenkontrollierten Bedingungen gezüchtet und aufgezogen werden, so daß man gesunde Versuchstiere hat, deren Abstammung bekannt ist. Diese Fische sind in vielen Teilen der Welt verfügbar.
Anhang 3 zur RL 67/548/EWG Anhang V C.13.
Vorhersage der Dauer der Aufnahme- und der Abbauphase
1 Vorhersage der Dauer der Aufnahmephase
Vor der Durchführung des Tests kann ein geschätzter Wert k2 und damit ein prozentualer Teil der für die Erreichung des Fließgleichgewichts benötigten Zeit aus den empirischen Beziehungen zwischen k2 und dem n-Oktanol/Wasser-Verteilungskoeffizienten (Pow) bzw. zwischen k2 und der Wasserlöslichkeit (s) abgeleitet werden.
So läßt sich k2 (Tag-1) beispielsweise anhand folgender empirischer Beziehung (1) schätzen:
log10k2 = -0,414 log10(Pow) + 1,47 (r2 = 0,95) (Gleichung 1)
Für weitere Beziehungen siehe Literaturhinweise (2).
Ist der Verteilungskoeffizient (Pow) nicht bekannt, kann dieser (3) anhand der bekannten Wasserlöslichkeit (s) der Substanz geschätzt werden:
log10(Pow) = 0,862 log10(s) + 0,710 (r2 = 0,994) (Gleichung 2)
wobei s = Löslichkeit (Mol/l) : (n = 36)
Diese Beziehungen gelten nur für Chemikalien mit log Pow-Werten zwischen 2 und 6,5 (4).
Die Zeit bis zur Einstellung eines gewissen Prozentsatzes des Fließgleichgewichts kann - durch Anwendung des Schätzwertes k2 - aus der allgemeinen kinetischen Gleichung, die die Aufnahme und die Ausscheidung (Kinetik erster Ordnung) beschreibt, abgeleitet werden:
dCf / dt = k1⋅ Cw - k2 ⋅ Cf
oder, wenn Cw konstant ist:
Cf = k1/ k2 ⋅ Cw (1 - e-k2t) (Gleichung 3)
Bei Annäherung an das Fließgleichgewicht (t →∞) kann Gleichung 3 reduziert werden (5) (6) zu:
Cf = k1 / k2 ⋅ Cw oder Cf/Cw = k1/k2 = BCF
Damit stellt (k1/k2) ⋅ Cw eine Annäherung an die Konzentration in den Fischen im "Fließgleichgewicht" (Cf,s) dar.
Gleichung 3 kann umgeformt werden in:
Cf = Cf,s (1 - e-k2t) oder Cf / Cfs = 1 - e-k2t (Gleichung 4)
Bei Anwendung von Gleichung 4 kann die Zeit bis zur Herstellung eines gewissen Gleichgewichtsprozentsatzes vorhergesagt werden, wenn k2 zuvor anhand der Gleichungen 1 oder 2 geschätzt wurde.
Als Richtschnur gilt, daß die statistisch optimale Dauer der Aufnahmephase für die Ableitung statistisch brauchbarer Daten (BCFk) die Zeit ist, die benötigt wird, bis die gegen die lineare Zeit aufgetragene Logarithmuskurve der Prüfsubstanzkonzentration in den Fischen ihren Mittelpunkt bzw. 1,6/k2 oder ein 80 %iges Fließgleichgewicht, jedoch nicht mehr als 3,0/k2 oder 95 %iges Fließgleichgewicht (7) erreicht.
Die Zeit zur Herstellung eines 80 %igen Fließgleichgewichts entspricht (Gleichung 4):
0,80 = 1 - e-k2t80 oder t80 = 1,6 / k2 (Gleichung 5)
Dementsprechend gilt für ein 95 %iges Fließgleichgewicht:
t95 = 3,0 / k2 (Gleichung 6)
Demnach wäre beispielsweise die Dauer der Aufnahmephase (ap) für eine Prüfsubstanz mit log Pow = 4 (unter Anwendung der Gleichungen 1, 5, 6):
log10k2 = -0,414 ⋅ (4) + 1,47 k2 = 0,652 Tage-1
ap (80 %) = 1,6 / 0,652, d.h. 2,45 Tage (59 Stunden)
oder ap (95 %) = 3,0 / 0,652; d. h. 4,60 Tage (110 Stunden).
Für eine Prüfsubstanz mit s = 10-5 Mol/l (log(s) = -5,0) wäre die Dauer der ap (unter Anwendung der Gleichungen 1, 2, 5, 6) entsprechend:
log10 (Pow) = -0,862 7 ⋅ (-5,0) + 0,710 = 5,02
log10k2 = -0,414 ⋅ (5,02) + 1,47
k2 = 0,246 Tage-1
ap (80 %) = 1,6 / 0,246; d.h. 6,5 Tage (156 Stunden)
oder ap (95 %) = 3,0 / 0,246; d.h. 12,2 Tage (293 Stunden)
Alternativ kann der Ausdruck:
teq = 6,54 ⋅ 10-3 Pow + 55,31 (Stunden)
zur Berechnung der Zeit bis zur Herstellung des effektiven Fließgleichgewichts verwendet werden (4).
2 Vorhersage der Dauer der Ausscheidungsphase
Die Vorhersage der Zeit, die für die Reduzierung der Körperbelastung auf einen gewissen Prozentsatz der ursprünglichen Konzentration benötigt wird, kann auch aus der allgemeinen kinetischen Gleichung erster Ordnung über die Aufnahme und die Ausscheidung (1) (8) abgeleitet werden.
Für die Ausscheidungsphase wird Cw als Null angenommen. Die Gleichung kann reduziert werden zu:
dCf / dt = -k2Cf oder Cf = Cf,0 ⋅ e-k2t
wobei Cf,0 die Konzentration zu Beginn der Ausscheidungsperiode bezeichnet. Eine 50 %ige Ausscheidung wird dann erreicht bei (t50):
Cf / Cf,0 = 1/2 = e-k2t50 oder t50 = 0,693 / k2
Dementsprechend wird eine 95 %ige Ausscheidung erreicht bei:
t95 = 3,0 / k2
Bei einer 80 %igen Aufnahme in der ersten Periode (1,6/k2) und einem 95 %igen Verlust in der Ausscheidungsphase (3,0/k2) wird die Ausscheidungsphase ungefähr doppelt solange wie die Aufnahmephase dauern.
Es ist jedoch wichtig festzuhalten, daß die Schätzungen auf der Annahme beruhen, daß die Aufnahme- und Ausscheidungsmuster einer Kinetik erster Ordnung folgen. Wenn es sich jedoch offensichtlich nicht um eine Kinetik erster Ordnung handelt, müssen komplexere Modelle verwendet werden (z.B. Literaturhinweis (1)).
Literaturhinweise (zu Anhang 3)
(1) Spacie A. and Hamelink J.L. (1982) Alternative models for describing the bioconcentration of organics in fish. Environ. Toxicol. and Chem. 1 S. 309-320.
(2) Kristensen P. (1991) Bioconcentration in fish: comparison of BCF's derived from OECD and ASTM testing methods; inflünce of particulate matter to the bioavailability of chemicals. Danish Water Quality Institute.
(3) Chiou C.T. and Schmedding D.W. (1982) Partitioning of organic compounds in octanol-water systems. Environ. Sci. Technol. 16 (1) S. 4-10.
(4) Hawker D.W. and Connell D.W. (1988) Influence of partition coefficient of lipophilic compounds on bioconcentration kinetics with fish. Wat. Res. 22 (6) S. 701-707.
(5) Branson D.R., Blau G.E., Alexander H.C. and Neely W.B. (1975) Transactions of the American Fisheries Society, 104 (4) S. 785-792.
(6) Ernst W. (1985) Accumulation in Aquatic Organisms. In: Appraisal of tests to predict the environmental behaviour of chemicals. Ed. by Sheehman P., Korte F., Klein W. and Bourdeau P.H. Part 4.4 S. 243-255. SCOPE, 1985, John Wiley & Sons Ltd. N.Y.
(7) Reilly P.M., Bajramovic R., Blau G.E., Branson D.R. and Sauerhoff M.W. (1977) Guidelines for the optimal design of experiments to estimate parameters in first order kinetic models, Can. J. Chem. Eng. 55 S. 614-622.
(8) Könemann H. and Van Leeuwen K. (1980) Toxicokinetics in Fish: Accumulation and Elimination of six Chlorobenzenes by Guppies. Chemosphere, 9 S. 3-19.
Anhang 4 zur RL 67/548/EWG Anhang V C.13.
Theoretisches Beispiel für einen Probenahmeplan für Biokonzentrationstests bei Substanzen mit log Pow =4
| Probenahme Fische |
Probenahmezeitplan | Anzahl der Wasserproben |
Anzahl der Fische pro Probe |
|||
| Erforderliche Mindesthäufigkeit (Tage) |
Zusätzliche Probenahmen |
|||||
| Aufnahme- phase |
- 1 0 |
2 * 2 |
Zugabe von 45-80 Fische |
|||
| 1. | 0,3 | 0,4 | 2 (2) |
4 (4) |
||
| 2. | 0,6 | 0,9 | 2 (2) |
4 (4) |
||
| 3. | 1,2 | 1,7 | 2 (2) |
4 (4) |
||
| 4. | 2,4 | 3,3 | 2 (2) |
4 (4) |
||
| 5. | 4,7 | 2 | 6 | |||
| Ausschei- dungsphase |
Umsetzung der Fische in Wasser ohne die Prüfchemikalie |
|||||
| 6. | 5,0 | 5,3 | 4 (4) |
|||
| 7. | 5,9 | 7,0 | 4 (4) |
|||
| 8. | 9,3 | 11,2 | 4 (4) |
|||
| 9. | 14,0 | 17,5 | 6 (4) |
|||
| *) Probewasser nachdem mindestens 3 "Kammer-lnhalte" geliefert wurden.
Die Werte in Klammern bezeichnen die Anzahl der Proben (Wasser, Fisch),
|
||||||
Anhang 5 zur RL 67/548/EWG Anhang V C.13.
Modelldiskriminierung
Man geht davon aus, daß die meisten Biokonzentrationsdaten durch ein einfaches Zwei-Kompartiment- /Zwei-Parameter- Modell "einigermaßen" gut dargestellt werden, wie aus der geradlinigen Kurve ersichtlich ist, die sich den Punkten für die Konzentrationen in den Fischen während der Ausscheidungsphase annähert, wenn diese auf semilogarithmischem Papier aufgetragen werden. (Wenn diese Punkte nicht durch eine geradlinige Kurve beschrieben werden können, sollten komplexere Modelle verwendet werden, siehe z.B. Spacie und Hamelink, Literaturhinweis 1 in Anhang 3).
Graphische Methode zur Bestimmung der Ausscheidungskonstanten k2
Tragen Sie die in den einzelnen Fischproben festgestellten Prüfsubstanzkonzentrationen gegen die Probenahmezeit auf semilogarithmischem Papier ab. Die Neigung dieser Linie bezeichnet k2.
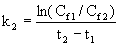
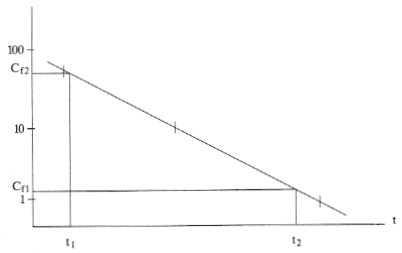
Beachten Sie, daß Abweichungen von einer geraden Linie auf ein komplexeres Ausscheidungsmuster als eine Kinetik erster Ordnung hindeuten können. Für eine Auswertung von Ausscheidungsvorgängen, die nicht einer Kinetik erster Ordnung entspricht, kann eine graphische Methode gewählt werden.
Graphische Methode zur Bestimmung der Aufnahmekonstanten k1
Bei gegebenem K2 wird k1 wie folgt berechnet:
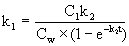 (Gleichung 1)
(Gleichung 1)
Der Wert Cf wird vom Mittelpunkt der glatten Aufnahmekurve abgelesen, die entsteht, wenn die log Konzentration gegen die Zeit (auf einer arithmetischen Skala) aufgetragen wird.
Computergestütztes Verfahren zur Berechnung der Aufnahme- und Ausscheidungskonstanten
Für die Berechnung des Biokonzentrationsfaktors sowie der Geschwindigkeitskonstanten k1 und k2 wird der Einsatz computergestützter, nichtlinearer Verfahren zur Parameterschätzung bevorzugt. Diese Programme bestimmen die Werte k1 und k2 basierend auf einem gegebenen Satz von über die Zeit ermittelten Konzentrationsdaten und dem Modell:
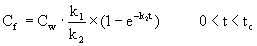 (Gleichung 2)
(Gleichung 2)
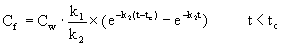 (Gleichung 3)
(Gleichung 3)
wobei tc die Zeit am Ende der Aufnahmephase bezeichnet.
Durch diesen Ansatz wird die Standardabweichung von k1 und k2 geschätzt.
Da k2 zumeist anhand der Ausscheidungskurve mit relativ hoher Genauigkeit geschätzt werden kann und weil es eine starke Korrelation zwischen den beiden Parametern k und k2 gibt, wenn sie gleichzeitig geschätzt werden, kann es u.U. ratsam sein, k2 zunächst lediglich anhand der Ausscheidungsdaten abzuleiten und anschließend k1 anhand der Aufnahmedaten mittels nichtlinearer Regression zu berechnen.
 |
weiter . |  |
(Stand: 08.08.2022)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: 90.- € netto (Grundlizenz)
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion
...
X
⍂
↑
↓